Приближенные решения

Точное решение

Дифференциальное уравнение равновесия имеет вид

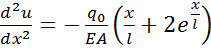(1.1)

Дважды интегрируем

(1.2)

(1.3)

Удовлетворяем геометрическому граничному условию на левом торце

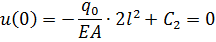
откуда

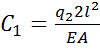(1.4)

Удовлетворяем статические граничные условия на правом торце

откуда

(1.5)

Внося полученные константы интегрирования (1.4) и (1.5) в (1.3), приходим к выражению для продольного перемещения

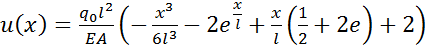(1.6)

Умножая на EA и беря производную по х для (1.6), получим выражение для нормального усилия

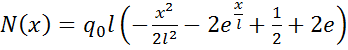(1.7)

Произведем расчеты перемещений и усилий по формулам (1.6) и (1.7) с помощью программы на языке программирования «Pascal» в пяти равноотстоящих точках и сведем результаты расчета в таблицу 1.

Program STTR;

uses crt;

Const

q=1.0; EA=1.0; l=1.0; m=4;

Var

i: integer;

dx, x, x2, nn, uu: real;

U, N: array [1..m+1] of real;

BEGIN

clrscr;

writeln;

writeln('Результаты расчета');

writeln;

writeln ('Координата Перемещение Усилие');

dx: =l/m;

nn: =q*l;

uu: = nn*l/EA;

for i: =1 to m+1 do begin

x: =dx*(i-1)/l;

x2: = sqr(x);

U[i]: =-x*x2/6 - 2*exp(x)+x*(0.5 + 2*exp(1)) + 2;

N[i]: =-x2/2-2*exp(x) + 0.5 + 2*exp(1);

writeln;

writeln('x=', x: 4: 4, 'U=', U[i]: 6: 3, 'N=', N[i]: 6: 3);

end;

readln;

END.

Представим результаты расчета в виде таблицы 1 и графиков (рис. 2 и 3)

Таблица 1

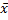
		0, 25	0, 5	0, 75
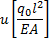
		0, 913	1, 650	2, 148	2, 333
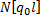
	3, 937	3, 337	2, 514	1, 421

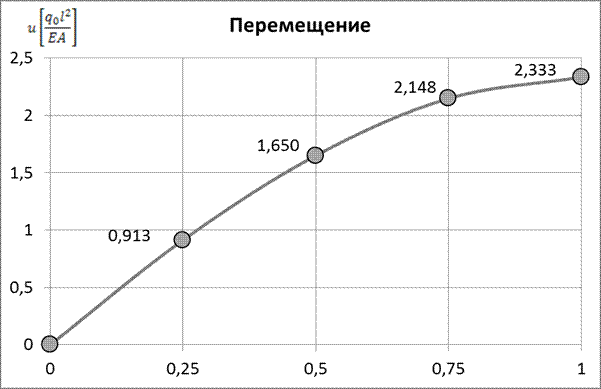
Рис.2 Изменение перемещения по длине стержня (точное решение)

Рис.3 Изменение продольного усилия по длине стержня (точное решение)

Приближенные решения