Метод конечных элементов

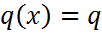₀

		x

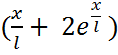
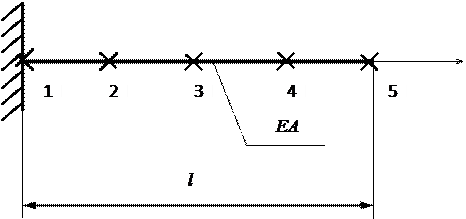
Разбиение стержня на элементы

Для отдельного конечного элемента матрица жесткости имеет вид:

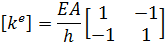
(2.3.1)

Матрица преобразования нагрузки (грузовая матрица) –

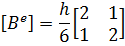
(2.3.2)

Вектор внешних нагрузок:

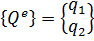
(2.3.3)

Матричное уравнение метода перемещений в конечноэлементной форме

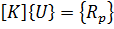
(2.3.4)

Здесь: матрица жесткости всей системы - 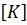, формирующаяся в соответствии с топологией системы; вектор неизвестных узловых перемещений - 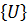; грузовой вектор системы –

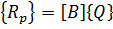
(2.3.5)

содержащий грузовую матрицу системы - 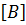и вектор внешних нагрузок системы - .

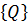Учитывая число участков (конечных элементов), запишем (2.3.4) для нашего примера в раскрытом виде:

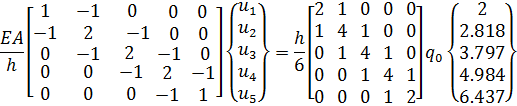
(2.3.6)

Умножая матрицу преобразования на вектор узловых значений нагрузки, перепишем (2.3.6) в виде:

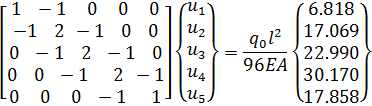
(2.3.7)

Геометрическое граничное условие (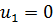) учтем, обнуляя строку и столбец с общим диагональным элементом – множителем при 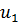(сам диагональный элемент при этом не обнуляется) и соответствующие элементы грузового вектора. Система (2.3.7) приобретает окончательный вид:

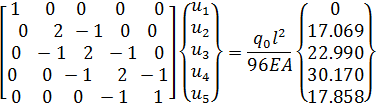
(2.3.8)

Выполним прямой ход снизу:

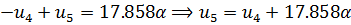
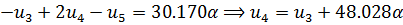
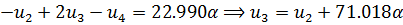
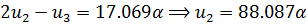
(2.3.9)

Выполним обратный ход, приводя к размерности точного решения

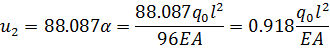
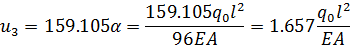
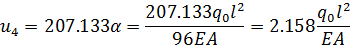
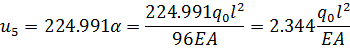
(2.3.10)

Осуществим переход к нормальным усилиям с помощью соотношения:

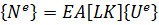
(2.3.11)

Первый элемент:

(2.3.12)

Второй элемент:

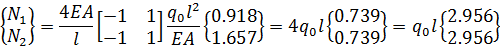
(2.3.13)

Третий элемент:

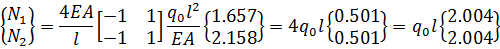
(2.3.14)

Четвертый элемент:

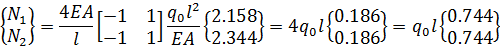
(2.3.15)

Воспользуемся дифференцирующей матрицей

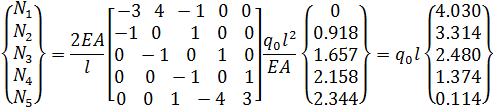
(2.3.16)

Результаты расчета представим в виде таблицы 4 и графиков (рис. 9, 10).

Таблица 5

		0, 25	0, 5	0, 75
		0, 918	1, 657	2, 158	2, 344
(0)	(0, 913)	(1, 650)	(2, 148)	(2, 333)
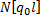
	3, 672*	2, 956*	2, 004*	0, 744*	-
4, 030**	3, 314**	2, 480**	1, 374**	0, 114**
(3, 937)	(3, 337)	(2, 514)	(1, 421)	(0)

(…) – точное решение; ^* - решение в рамках МКЭ; ^** - решение с помощью дифференцирующей матрицы.

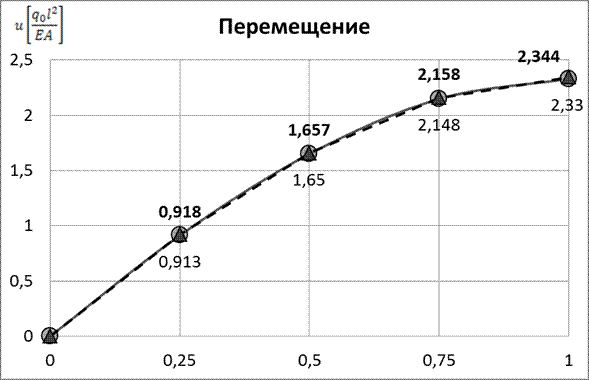
Рис.9 Изменение перемещения по длине стержня (метод конечных элементов)

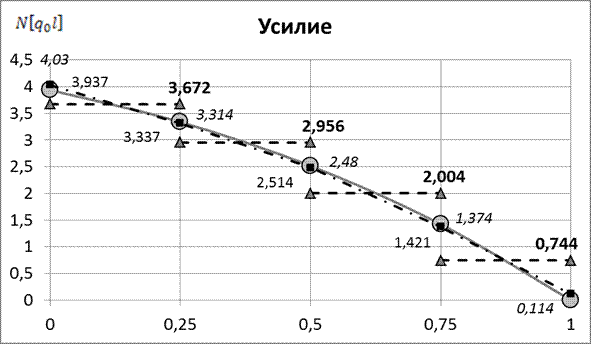
Рис.10 Изменение продольного усилия по длине стержня (метод конечных элементов)