
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод конечных разностей
|
|
Обозначим узловые точки (1 – 5) в местах разбиения стержня на четыре элемента и введем законтурную точку 6 (рис.4).
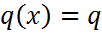 0
0 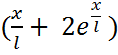
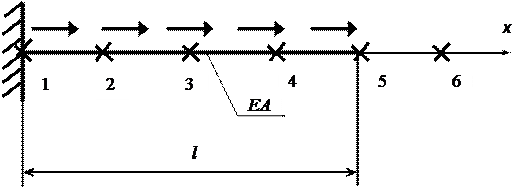 |
Рис. 4. Разбиение стержня на элементы
Запишем дифференциальное уравнение в конечно – разностной форме
 (2.1.1)
(2.1.1)
Здесь введено обозначение
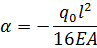
Запишем уравнения для всех внутренних точек, причем для крайней правой точки 5 запишем статической граничное условие через законтурную точку 6:
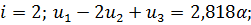
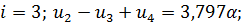
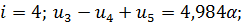
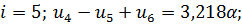
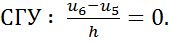 (2.1.3)
(2.1.3)
Выполним прямой ход, учитывая левое геометрическое граничное условие (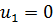 ):
):

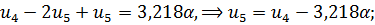
|
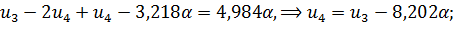
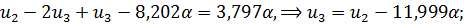
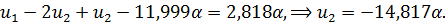
|
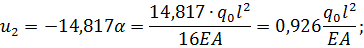

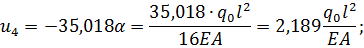
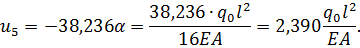
Осуществим переход к нормальным усилиям с учетом размерностей для перемещений и усилий в точном решении при помощи соотношения
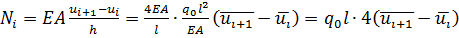 , (2.1.6)
, (2.1.6)
где черта над u обозначает, что берутся только ее численные значения.
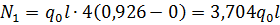
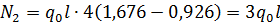 (2.1.7)
(2.1.7)
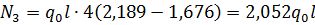
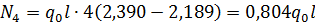
Воспользуемся соотношением, осуществляющим переход к усилиям с помощью дифференцирующей матрицы
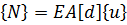 (2.1.8)
(2.1.8)
Которое в раскрытом виде с учетом числа элементов (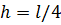 ) и размерностей, использованных для перемещений и усилий в точном решении, запишется так:
) и размерностей, использованных для перемещений и усилий в точном решении, запишется так:
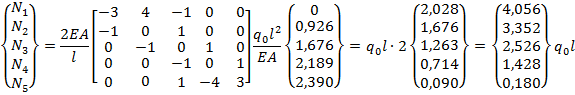
(2.1.9)
Результаты представим в виде таблицы 2 и графиков (рис. 5, 6).
Таблица 2
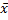
| 0, 25 | 0, 5 | 0, 75 | ||
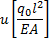
| 0, 926 | 1, 676 | 2, 189 | 2, 39 | |
| (0) | (0, 913) | (1, 650) | (2, 148) | (2, 333) | |
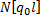
| 3, 704* | 3* | 2, 048* | 0, 804* | - |
| 4, 056** | 3, 352** | 2, 524** | 1, 426** | 0, 182** | |
| (3, 937) | (3, 337) | (2, 514) | (1, 421) | (0) |
(…) – точное решение; * - решение в рамках МКР; ** - решение с помощью дифференцирующей матрицы.

Рис.5 Изменение перемещения по длине стержня (метод конечных разностей)

Рис.6 Изменение продольного усилия по длине стержня (метод конечных разностей)
2.2 Метод Бубнова – Галеркина.
Аппроксимирующую функцию для варианта В запишем в виде:
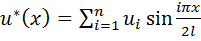 (2.2.1)
(2.2.1)
Дифференциальное уравнение имеет вид

Внесем аппроксимирующую функцию в дифференциальное уравнение
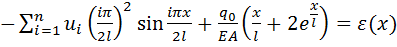 (2.2.2)
(2.2.2)
Умножим (2.2.2) почленно на 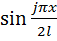 и проинтегрируем от 0 до
и проинтегрируем от 0 до 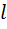
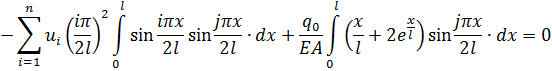
(2.2.3)
В силу ортогональности

(2.2.4)
Возьмем остальные интегралы (берем интегралы по частям)

(2.2.5)
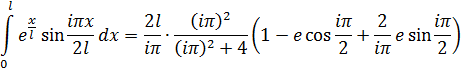
(2.2.6)
Внесем (2.2.4) – (2.2.6) в (2.2.3) и получим
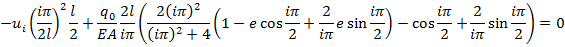
(2.2.7)
Откуда
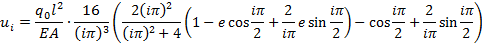
(2.2.8)
Выражение для перемещения приобретает вид:

(2.2.9)
Для усилия на основании равенства
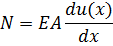
Получаем следующее соотношение:
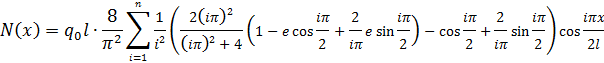
(2.2.10)
Программа для численной реализации (2.2.9) и (2.2.10):
Program BH;
uses crt;
Const
q=1.0; EA=1.0; l=1.0; m=4; mn=10;
Var
i, j, k: integer;
dx, x, nn, uu, un, p2, px, p, i2, ip2: real;
U, N: array [1..m+1] of real;
BEGIN
clrscr;
dx: =l/m;
nn: =q*l;
uu: = nn*l/EA;
writeln;
writeln('Результаты решения методом Бубнова-Галеркина');
writeln;
writeln ('Координата Перемещение Усилие');
for k: =1 to m+1 do begin
x: =dx*(k-1)/l;
U[k]: =0;
N[k]: =0;
for j: =1 to mn do begin
i: =2*j-1;
p: =i*pi;
p2: =p/2;
ip2: =2*sqr(p)/(4+sqr(p));
px: =p2*x;
un: =(ip2*(1-exp(1)*cos(p2)+2/p*exp(1)*sin(p2))-cos(p2)+2/p*sin(p2))/sqr(i);
N[k]: =N[k]+un*cos(px)*8/pi/pi;
U[k]: =U[k]+un*sin(px)/i*16/pi/pi/pi;
end;
writeln;
writeln('x=', x: 5: 2, 'U=', U[k]: 6: 3, 'N=', N[k]: 6: 3);
end;
readln;
END.
Результаты расчета при удержании 10 членов ряда представим в виде таблицы 3 и графиков (рис. 7, 8).
Таблица 3
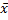
| 0, 25 | 0, 5 | 0, 75 | ||
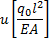
| 0, 913 | 1, 650 | 2, 148 | 2, 333 | |
| (0) | (0, 913) | (1, 650) | (2, 148) | (2, 333) | |
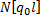
| 3, 937 | 3, 337 | 2, 514 | 1, 421 | |
| (3, 896) | (3, 342) | (2, 515) | (1, 419) | (0) |
(…) – точное решение.
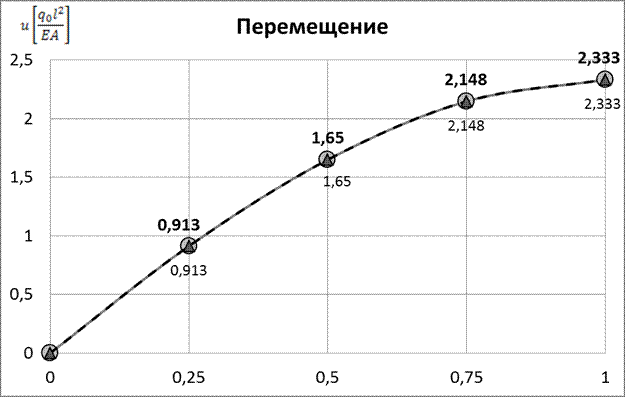
Рис.7 Изменение перемещения по длине стержня (метод Бубнова – Галеркина, 10 членов ряда)
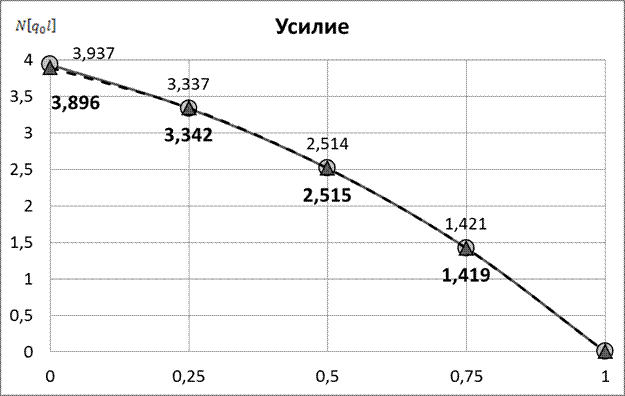
Рис.8 Изменение продольного усилия по длине стержня (метод Бубнова – Галеркина, 10 членов ряда)