
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Преобразования десятичных дробей
|
|
Выражение десятичных дробей в более крупных (мелких) долях
(сокращение дробей) (7 класс)
Учащимся предлагается показать 0, 4 и 0, 40 на метровой линейке, разделенной на дециметры и сантиметры соответственно. Они вспоминают, что 0, 4 м = 0, 40 м (см выше). Аналогичная работа проделывается с использованием квадрата. Далее школьникам предлагается записать дробь 0, 40 со знаменателем: 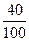 . Очевидно, что дробь можно сократить на 10:
. Очевидно, что дробь можно сократить на 10:
0, 40 = 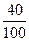 =
= 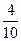 = 0, 4, т.е. 0, 40 = 0, 4.
= 0, 4, т.е. 0, 40 = 0, 4.
Учащиеся отмечают, что в процессе преобразования не стало нуля, получились более крупные доли, но значение дроби не изменилось. Вводится правило: если в десятичной дроби отбросить один нуль после значащей цифры, то значение этой дроби не изменится.
Данное правило закрепляется на примерах. Например, дана дробь 1, 20. Эта дробь иллюстрируется при помощи рулетки.
1, 20 – это 1 м и 20 см или 1, 20 м;
1, 20 – это 1 м 2 дм и 1, 2 м, значит 1, 20 м = 1, 2 м. дроби записываются без наименований: 1, 20 = 1, 2. Вновь формулируется правило.
Далее сокращение дробей иллюстрируется на основе сокращения обыкновенных дробей:
1, 20 = 1 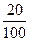 = 1
= 1 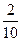 = 1, 2, т.е. 1, 20 = 1, 2.
= 1, 2, т.е. 1, 20 = 1, 2.
Аналогично рассматривается еще несколько примеров, после чего школьники применяют правило самостоятельно: 2, 40 = 2, 4; 17, 30 = 17, 3 и т.д.
Подобным образом вводится сокращение десятичных дробей на 100 и 1000. Формулируется обобщенное правило: если десятичная дробь оканчивается одним или несколькими нулями, то эти нули можно отбросить - получится дробь, равная данной (или значение дроби не изменится).
В учебнике 6 кл. дается следующее правило: чтобы десятичную дробь выразить в более крупных долях, нужно отбросить нули в конце записи десятичной дроби.
Правило выражения дробей в более мелких долях вводится аналогично вышеописанному правилу. Школьники убеждаются в том, что нуль, приписанный справа, не меняет значение дроби: 0, 4 = 0, 40 = 0, 400. При этом увеличивается и числитель, и знаменатель в одно и то же число раз (можно показать, используя обыкновенные дроби:  ). Учащиеся отмечают, что доли становятся мельче, но значение дробей не меняется. Таким образом, формулируется правило: если к десятичной дроби приписать справа один или несколько нулей, то получится дробь, равная данной (или: значение дроби не изменится).
). Учащиеся отмечают, что доли становятся мельче, но значение дробей не меняется. Таким образом, формулируется правило: если к десятичной дроби приписать справа один или несколько нулей, то получится дробь, равная данной (или: значение дроби не изменится).
Выражение десятичных дробей в одинаковых долях
(приведение дробей к общему знаменателю) (7 класс)
Учащиеся с нарушением интеллекта часто затрудняются при сравнении дробей с разными знаменателями, поскольку слабо дифференцируют разрядные единицы и не осознают, какие доли надо сравнивать между собой. Ошибки возникают и при выполнении действий сложения и вычитания дробей с разными знаменателями. Для удобства вычислений и сравнения дроби выражают в одинаковых долях, т.е. приводят их к наименьшему общему знаменателю.
Например, необходимо выразить в одинаковых долях дроби 0, 3 и 0, 25. Проводится следующая работа:
- Назовите дроби.
- Назовите знаменатель первой дроби (10).
- Назовите знаменатель второй дроби (100).
- Эти дроби надо выразить в одинаковых долях, то есть уравнять количество знаков после запятой. (Уточняется, что дробь 0, 25 нельзя выразить в десятых долях, так как после запятой имеются две значащие цифры).
- Выразим в сотых долях дробь 0, 3. Что для этого надо сделать? (приписать справа один нуль).
- 0, 3 = 0, 30. Значение дроби 0, 3 не изменилось, но доли стали мельче (были десятые, а стали сотые).
- Дроби 0, 30 и 0, 25 теперь имеют одинаковый знаменатель – 100. Мы уравняли количество знаков после запятой, приписав к дроби 0, 3 один нуль справа.
Далее выполняются тренировочные упражнения по выражению дробей в одинаковых долях (или приведению дробей к общему знаменателю): 5, 4 и 6, 18; 8, 30 и 3, 2 и т.д.
С целью дифференциации всех изученных преобразований следует предлагать различные упражнения:
1. Сократить дробь: 24, 30; 155, 700; 4, 040 и т.д.
2. Выразить дроби в более мелких долях: 2, 6; 65, 03; 22, 78 и т.д.
3. Привести дроби к общему знаменателю: 5, 2 и 6, 300; 24, 05 и 13, 1; 10, 9 и 10, 999 и т.д.
Замена десятичной дроби обыкновенной и наоборот.
Дроби конечные и бесконечные (периодические) (9 класс)
Учащиеся постоянно сталкивались с выражением десятичной дроби в виде обыкновенной. Это выражение заключается в записи десятичной дроби со знаменателем:
0, 5 = 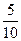 ; 2, 23 = 2
; 2, 23 = 2 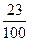 и т.д.
и т.д.
Если в знаменателе обыкновенной дроби содержится 1 с нулями, то дробь легко можно записать в виде десятичной: 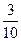 = 0, 3. Однако не всегда знаменатель обыкновенной дроби равен 10. 100, 1000 и т.д.
= 0, 3. Однако не всегда знаменатель обыкновенной дроби равен 10. 100, 1000 и т.д.
Например, в дроби 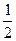 знаменатель равен 2. Чтобы дробь была десятичной, ее знаменатель должен быть равен 10, 100, 1000 и т.д. Следовательно из знаменателя 2 надо получить такое число, которое будет представлять собой единицу с одним или несколькими нулями. Чтобы получить число 10, надо число 2 умножить на 5: 2 х 5 = 10.
знаменатель равен 2. Чтобы дробь была десятичной, ее знаменатель должен быть равен 10, 100, 1000 и т.д. Следовательно из знаменателя 2 надо получить такое число, которое будет представлять собой единицу с одним или несколькими нулями. Чтобы получить число 10, надо число 2 умножить на 5: 2 х 5 = 10.
Чтобы значение дроби не изменилось надо и числитель и знаменатель умножить на 5, т.е. 5 –дополнительный множитель к дроби 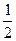 . Таким образом:
. Таким образом: 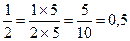 .
.
Дробь  нельзя выразить в десятых долях, т.к. 10 не делится нацело на 4. поэтому следует предложить школьникам попробовать выразить ее в сотых долях. 100: 4 = 25, следовательно дробь
нельзя выразить в десятых долях, т.к. 10 не делится нацело на 4. поэтому следует предложить школьникам попробовать выразить ее в сотых долях. 100: 4 = 25, следовательно дробь  можно выразить в сотых долях. Для этого и числитель и знаменатель этой дроби надо умножить на 25:
можно выразить в сотых долях. Для этого и числитель и знаменатель этой дроби надо умножить на 25:  .
.
Аналогично рассматривается выражение обыкновенной дроби в тысячных долях.
Вместе с тем использование описанного способа не всегда возможно. Поэтому школьникам предлагается второй способ выражения обыкновенной дроби десятичной. Учащиеся вспоминают, что черта дроби обозначает деление, следовательно любая дробь представляет собой частное от деления числителя на знаменатель. Например, дробь  можно рассматривать как частное от деления 1 на 4.
можно рассматривать как частное от деления 1 на 4.
 Школьники учатся рассуждать:
Школьники учатся рассуждать:
 1 4 1 на 4 не делится нацело, поэтому в частном
1 4 1 на 4 не делится нацело, поэтому в частном
_10 0, 25 пишем нуль целых и отделяем целую часть
8 запятой. Дробим 1 в десятые доли – получаем
_20 10 десятых. 10 десятых делим на 4. Получаем
20 2 десятых. 2 десятых пишем в частном. 10 деся-
0 тых минус 8 десятых получится 2 десятых. В
остатке пишем 2 десятых дробим 2 десятые в сотые – получаем 20 сотых. 20 сотых делим на 4 – получаем 5 сотых. 5 сотых записываем в частное. Итого в частном 0, 25. Следовательно  = 0, 25.
= 0, 25.
На основе рассмотрения ряда примеров учащиеся подводятся к выводу: если в знаменателе обыкновенной дроби стоит не единица с нулями, а какое-нибудь другое число, то для получения десятичной дроби надо числитель обыкновенной дроби разделить на ее знаменатель.
Учащимся следует показать, что деление числителя на знаменатель не всегда заканчивается, то есть познакомить их с понятиями конечная и бесконечная десятичная дробь. Для этого предлагается выразить дробь 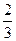 в виде десятичной дроби.
в виде десятичной дроби.
 2 3 Учащиеся убеждаются в том, что в остатке по-
2 3 Учащиеся убеждаются в том, что в остатке по-
 _20 0, 666… стоянно остается 2, а в частном получается 6.
_20 0, 666… стоянно остается 2, а в частном получается 6.
18 Деление может продолжаться бесконечно.
_20 школьникам объясняется, что деление преры-
18 вают на каких-то долях. В данном случае закон-
_20 чили делить на тысячных долях. Многоточие
18 означает, что делить можно и далее. 0, 666… -
2 неточное, приближенное значение дроби 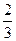 .
.
В аналогичных случаях (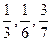 и т.д.) учащиеся получают приближенные значение дробей. На рассмотрении различных примеров они убеждаются в том, что некоторые обыкновенные дроби можно точно выразить десятичными – в этом случае получаются конечные десятичные дроби, а некоторые можно заменить только бесконечными десятичными дробями.
и т.д.) учащиеся получают приближенные значение дробей. На рассмотрении различных примеров они убеждаются в том, что некоторые обыкновенные дроби можно точно выразить десятичными – в этом случае получаются конечные десятичные дроби, а некоторые можно заменить только бесконечными десятичными дробями.
Запись чисел, полученных при измерении величин, десятичной дробью и наоборот – самостоятельно (с. 326-328).