
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
А) Методи розрахунку
|
|
Для розрахунку ЕДЗ використовуються два методи. У першому сила розглядається як результат взаємодії провідника ыз струмом в магнітному полі. Якщо елементарний провідник dL зі струмом і знаходиться в магнітному полі з індукцією В, що створюється іншими провідниками, то сила dF, що діє на цей елемент, дорівнює
dF=i dl x B= sB× dL× sinb,
де і – струм; b – кут між векторами елемента dL і індукцією В, що вимірюється кутом повороту вектора dL до вектора В за найменшою відстанню.
За напрямок вектора dL приймається напрямок струму в елементі. Напрямок індукції В, що створюється іншим провідником, визначається за правилом буравчика, а напрямок сили – за правилом лівої руки (рис.1). Для визначення повної сили, діючої на провідник довжиною L, необхідно просумувати, діючі на всі його елементи dL:
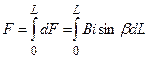 (1)
(1)
У випадку вільного розташування провідників в одній площині b=90° рівняння (1) спрощується:
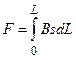 . (2)
. (2)
Рис.1 – до визначення електродинамічної сили.
Рис.2 – до визначення напрямку дії електродинамічної сили.
Рис.3 – до визначення напрямку дії електродинамічної сили в різних випадках розташування провідників.
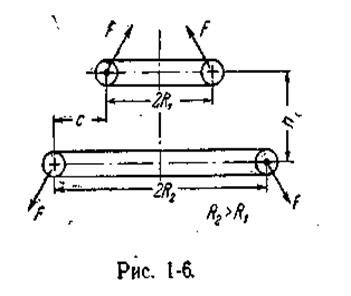
Рис.4 – до визначення ЕДЗ між двома витками або котушками.
Описаний метод рекомендується застосовувати тоді, коли можна аналітично знайти індукцію в будь-якій точці провідника, для якого необхідно визначити силу. Індукцію визначають, використовуючи закон Біо-Савара—Лапласа.
Другий метод базується на використанні енергетичного балансу системи провідників зі струмом. Якщо знехтувати енергетичною енергією системи і прийняти, що при деформації струмоведучих контурів або при їх переміщенні за дією ЕДЗ струми у всіх контурах залишаються незмінними, то сили можна найти за рівнянням
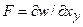 , (3)
, (3)
де W – електродинамічна енергія; ху – можливе переміщення в напрямку дії сили. Таким чином, сила дорівнює часній похідній від електромагнітної енергії даної системи за координатою, в напрямку якої діє сила. При розрахунку ЕДЗ, діючому при КЗ, величини струмів у контурах можна вважати незмінними.
Електромагнітна енергія системи зумовлена як енергією магнітного поля кожного ізольованого контуру, так і енергією, що визначається магнітним зв’язком між контурами і для двох взаємодіючих контурів дорівнює
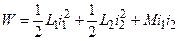 , (4)
, (4)
де L1, L2 – індуктивність контурів; і1, і2 – струми, що протікають в них; М – взаємна індуктивність.
Перші два члени рівняння визначають енергію незалежних контурів, а третій член дає енергію, зумовлену їх магнітним зв’язком.
Рівняння (4) дозволяє розрахувати як сили, діючі в ізольованому контурі, так й силу взаємодії контуру з усіма іншими. Для визначення сил всередині одного незалежного контуру використовують рівняння
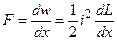 .
.
При розрахунку сили взаємодії контурів вважаємо, що енергія змінюється тільки в результаті зміни взаємного розташування контурів. При цьому енергія, зумовлена власною індуктивністю, вважається незмінною. У даному випадку сила між контурами дорівнює

 .
.
Енергетичний метод зручний, коли відома аналітична залежність індуктивності або взаємної індуктивності від геометричних розмірів.