
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определения и свойства сходящихся последовательностей.
|
|
Лекция 9. Сходящиеся последовательности.
Определения и свойства сходящихся последовательностей.
Определение 9.1. Последовательность 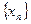 называется сходящейся, если существует такое число
называется сходящейся, если существует такое число 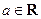 , что последовательность
, что последовательность  является бесконечно малой. При этом число а называется пределом последовательности
является бесконечно малой. При этом число а называется пределом последовательности  .
.
В силу определения любая бесконечно малая последовательность имеет пределом 0. Запись:  или
или  при
при 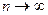 .
.
Определение 9.2. Последовательность 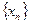 называется сходящейся, если
называется сходящейся, если 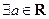 : для
: для 
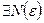 : при всех
: при всех 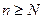
 .
.
Последнее неравенство означает, что элементы xn при 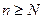 лежат в интервале
лежат в интервале  , который назовем
, который назовем 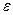 -окрестностью точки а.
-окрестностью точки а.
Определения 9.1 и 9.2 эквивалентны.
♦ Утверждение 9.1. Элемент xn сходящейся последовательности может быть представлен в виде 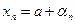 , где
, где 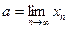 ,
, 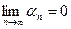 (
(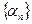 – бесконечно малая последовательность).
– бесконечно малая последовательность).
☼ Замечание 9.1. Последовательности, не являющиеся сходящимися, называют расходящимися. ☼
☼ Замечание 9.2. Будем считать, что бесконечно большие последовательности сходятся к пределу 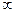 :
: 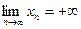 или
или  . ☼
. ☼
J Пример 9.1. Рассмотрим последовательность 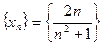 . Докажем, что
. Докажем, что 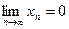 .
.
Доказательство. По определению 2 имеем
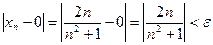 ,
, 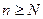 ;
; 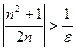 ;
; 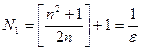 ;
;
если 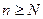 , то
, то 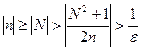 , где
, где 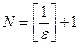 . Таким образом, начиная с номера
. Таким образом, начиная с номера 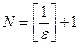 , выполняется неравенство
, выполняется неравенство  и
и  . ■ J
. ■ J
♦ Теорема 9.1. Сходящиеся последовательности имеют только один предел.
Доказательство. Пусть 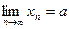 и
и 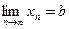
 .Тогда
.Тогда  ,
,  , где
, где 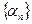 ,
,  – бесконечно малые последовательности. Получаем:
– бесконечно малые последовательности. Получаем: 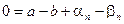 , все элементы бесконечно малой последовательности
, все элементы бесконечно малой последовательности 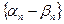 равны
равны 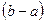 . Тогда по теореме 8.5
. Тогда по теореме 8.5 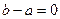 и b = a. ■
и b = a. ■
♦ Теорема 9.2. Всякая сходящаяся последовательность является ограниченной.
Доказательство. Пусть 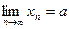 . Фиксируем
. Фиксируем 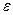 ,
, 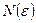 :
:  при
при 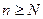 ,
, 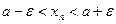 ,
, 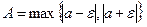 . Тогда
. Тогда 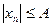 для
для  n. ■
n. ■
☼ Замечание 9.3. Не всякая ограниченная последовательность является сходящейся.
Например: 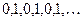 . ☼
. ☼