
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Предельный переход в неравенствах.
|
|
♦ Теорема 9.6. Если все элементы сходящейся последовательности  , начиная с некоторого номера, удовлетворяют неравенству
, начиная с некоторого номера, удовлетворяют неравенству 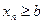
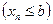 , то и предел
, то и предел 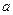 этой последовательности удовлетворяет неравенству
этой последовательности удовлетворяет неравенству 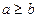
 .
.
Доказательство. Пусть при 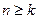 выполняется неравенство
выполняется неравенство 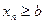 .
.
Предположим противное: пусть  . Положим
. Положим 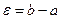 . При
. При 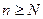
 , но тогда
, но тогда 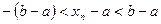

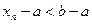 ,
,  – получается противоречие
– получается противоречие 
 (случай
(случай 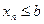 рассматривается аналогично). ■
рассматривается аналогично). ■
☼ Замечание 9.4. Элементы сходящейся последовательности  могут удовлетворять строгому неравенству
могут удовлетворять строгому неравенству  , однако при этом может оказаться a=b. Например, если
, однако при этом может оказаться a=b. Например, если 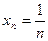 , то при
, то при 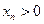 получаем
получаем  . ☼
. ☼
Следствие 1. Если элементы  и
и  сходящихся последовательностей
сходящихся последовательностей  и
и 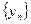 , начиная с некоторого номера, удовлетворяют неравенству
, начиная с некоторого номера, удовлетворяют неравенству  , то их пределы удовлетворяют такому же неравенству:
, то их пределы удовлетворяют такому же неравенству: 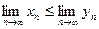 .
.
Действительно, если  , то
, то 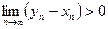

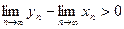 .
.
Следствие 2. Если все элементы сходящейся последовательности  находятся на сегменте
находятся на сегменте  , то и её предел с также находится на этом сегменте.
, то и её предел с также находится на этом сегменте.
Это очевидно: так как 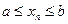 , то и
, то и 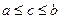 .
.
♦ Теорема 9.7 (принцип двустороннего ограничения). Пусть  и
и  – две сходящиеся последовательности, имеющие общий предел a. Пусть, кроме того, все элементы третьей последовательности
– две сходящиеся последовательности, имеющие общий предел a. Пусть, кроме того, все элементы третьей последовательности 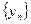 , по крайней мере начиная с некоторого номера, удовлетворяют неравенству
, по крайней мере начиная с некоторого номера, удовлетворяют неравенству  . Тогда последовательность
. Тогда последовательность 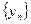 сходится и имеет предел a.
сходится и имеет предел a.
Доказательство. Достаточно доказать, что 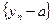 бесконечно малая последовательность. Пусть
бесконечно малая последовательность. Пусть 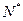 – номер, начиная с которого выполняется неравенство
– номер, начиная с которого выполняется неравенство  .Тогда, начиная с
.Тогда, начиная с  , выполняется и неравенство
, выполняется и неравенство  . Отсюда следует, что при
. Отсюда следует, что при 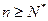
 .Фиксируем
.Фиксируем 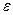 . Тогда
. Тогда

Обозначим 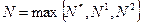 , тогда при
, тогда при 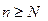
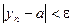 . ■
. ■