
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоремы об арифметических операциях над элементами сходящихся последовательностей.
|
|
♦ Теорема 9.3. Сумма (разность) сходящихся последовательностей 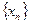 и
и 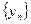 представляет собой сходящуюся последовательность, предел которой равен сумме (разности) пределов последовательностей
представляет собой сходящуюся последовательность, предел которой равен сумме (разности) пределов последовательностей 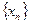 и
и 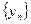 , то есть
, то есть  .
.
Доказательство. Пусть а и b – соответственно пределы последовательностей 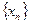 и
и 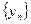 . Тогда
. Тогда 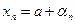 и
и 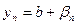 , где
, где 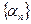 и
и  - бесконечно малые последовательности. Следовательно,
- бесконечно малые последовательности. Следовательно, 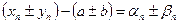 . Последовательность
. Последовательность 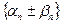 – бесконечно малая, таким образом, последовательность
– бесконечно малая, таким образом, последовательность 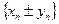 сходится и имеет своим пределом число
сходится и имеет своим пределом число  . ■
. ■
♦ Теорема 9.4. Произведение сходящихся последовательностей 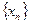 и
и 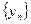 представляет собой сходящуюся последовательность, предел которой равен произведению пределов
представляет собой сходящуюся последовательность, предел которой равен произведению пределов 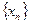 и
и 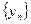 , то есть
, то есть  .
.
Доказательство. Пусть а и b – пределы последовательностей 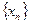 и
и 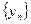 . Тогда
. Тогда 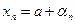 и
и 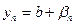 , где
, где 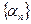 и
и  – бесконечно малые последовательности. Рассмотрим разность
– бесконечно малые последовательности. Рассмотрим разность  . Последовательность
. Последовательность 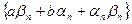 – бесконечно малая, тогда и последовательность
– бесконечно малая, тогда и последовательность 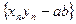 также бесконечно малая, поэтому последовательность
также бесконечно малая, поэтому последовательность 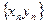 сходится и имеет своим пределом число
сходится и имеет своим пределом число 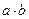 . ■
. ■
♦ Лемма 9.1. Если последовательность 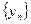 сходится к отличному от нуля пределу b, то, начиная с некоторого номера, определено частное
сходится к отличному от нуля пределу b, то, начиная с некоторого номера, определено частное 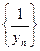 последовательностей
последовательностей  и
и 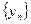 , которое представляет собой ограниченную последовательность.
, которое представляет собой ограниченную последовательность.
Доказательство. Пусть 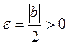 , т.к.
, т.к. 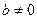 . Тогда
. Тогда 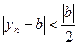 при
при 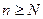 ,
,
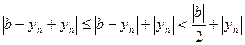

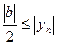
Значит, начиная с 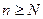 ,
, 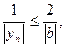 последовательность
последовательность 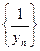 ограничена. ■
ограничена. ■
♦ Теорема 9.5. Частное двух сходящихся последовательностей  и
и 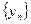 при условии, что
при условии, что  , есть сходящаяся последовательность, предел которой равен частному пределов последовательностей
, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей  и
и 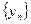 .
.
Доказательство. Пусть 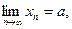
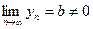 . По лемме при
. По лемме при 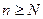
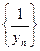 – ограниченная последовательность.
– ограниченная последовательность.
Рассмотрим при 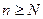 частное
частное  ; докажем, что
; докажем, что 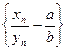 – бесконечно малая.
– бесконечно малая.
Рассмотрим разность
 .
.
Так как 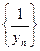 – ограниченная, а
– ограниченная, а 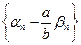 – бесконечно малая, то последовательность
– бесконечно малая, то последовательность 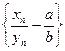 также бесконечно малая, значит, последовательность
также бесконечно малая, значит, последовательность  сходится и её предел
сходится и её предел 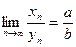 . ■
. ■
J Пример 9.2. 1) Найти  . При
. При 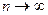 числитель и знаменатель стремятся к бесконечности и сразу применить теорему о пределе частного нельзя, так как в условии теоремы 9.5 предполагается существование конечных пределов. Преобразуем данную последовательность, разделив все члены дроби на
числитель и знаменатель стремятся к бесконечности и сразу применить теорему о пределе частного нельзя, так как в условии теоремы 9.5 предполагается существование конечных пределов. Преобразуем данную последовательность, разделив все члены дроби на  . Затем, применяя теоремы о пределе частного и о пределе суммы, найдём:
. Затем, применяя теоремы о пределе частного и о пределе суммы, найдём:
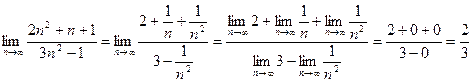 .
.
Когда вырабатывается определённый навык, подробную запись можно сократить.
2) Найти 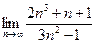 . Разделим все члены дроби на
. Разделим все члены дроби на 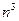 и используем необходимые теоремы:
и используем необходимые теоремы: 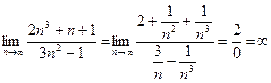 .
.
3) Найти 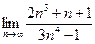 . Разделим все члены дроби на
. Разделим все члены дроби на 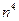 , получим:
, получим:  . J
. J
При решении задач можно воспользоваться результатами приведённых примеров. Сделаем вывод: если старшие степени n в числителе и знаменателе равны, то ответ равен отношению коэффициентов при данных степенях; если старшая степень n находится в числителе, то ответ будет 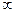 , если старшая степень – в знаменателе, то ответ будет 0.
, если старшая степень – в знаменателе, то ответ будет 0.