
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Рациональный выбор потребителя
|
|
Использование математического аппарата позволяет получать интересные интерпретации многих базовых понятий в теории потребления и в целом в микроэкономике.
Итак, будем считать, что каждый потребитель может определить свою функцию полезности – формулу, которая связывает величину общей полезности с набором благ. Например, предположим, Анна имеет функцию полезности относительно клубники (Х) и молока (У) следующего вида:

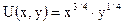
Предельная полезность блага Х (клубники) для Анны можно определить, применяя дифференциальное исчисление. Предельная полезность показывает, как изменится общая полезность Анны при увеличении потребления блага Х (клубники) на бесконечно малую величину, при условии, что объем потребления других благ остался без изменения:

Предельная полезность блага У (молока) определяется аналогично:

Предельная норма замещения может быть определена по формуле:
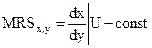
Если U = U(х, y), то изменение общей полезности при изменении х и у можно записать формулой:
dU = МUхdx + МUydy
Рассматривая кривую безразличия, отмечаем, что движение вдоль нее определяет dU = 0.
Тогда О = МUхdx + МUydy,

Минус перед отношением  показывает, что кривая безразличия имеет отрицательный наклон.
показывает, что кривая безразличия имеет отрицательный наклон.
Равновесный набор потребителя – это набор благ, который максимизирует значение функции полезности данного потребителя при имеющемся у него бюджете. Использование метода Лагранжа для решения этой задачи состоит в выполнении следующих этапов:
1. Записывается выражение Лагранжа.
Записывается функция полезности, которую нужно максимизировать плюс бюджетное ограничение, умноженное на l.
Z = U (х, y) + l (I – Рx ∙ x – Рy ∙ y),
где I – доход потребителя;
Рx, Ру – цены благ х и у;
I = Рx ∙ x + Ру ∙ y – бюджетное ограничение;
l – предельная полезность дохода (I), то есть дополнительная полезность, которую приносит дополнительный рубль:

2. Выражение Лагранжа дифференцируется по отношению к х, y, l. Полученные производные приравниваются к нулю.
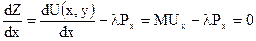
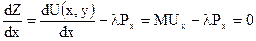
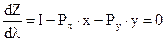
Эти уравнения можно записать в виде:
 МUх = lPх
МUх = lPх
МUy = lPy
Px ∙ x + Py ∙ y = I
3. Полученная система уравнений решается для х, y, l, а x и у представляют собой набор благ, максимизирующий полезность потребителя.
Пример
Анна имеет функцию полезности U(х, y) = x3/4 ∙ y1/4, I = 100, Рx = 1, Рy = 2. Тогда:
1. Выражение Лагранжа:
Z = x3/4 ∙ y1/4 + l (100 – 4 ∙ x – 2 ∙ y)
2. Дифференцируем выражение Лагранжа и приравниваем к нулю, полученные производные:

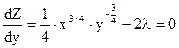


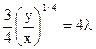 (*)
(*)
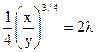 (**)
(**)
100 = 4х + 2у (***)
3. Решение системы уравнений.
Уравнение (*) делим на уравнение (**)
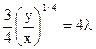

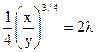

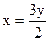
Полученное значение х подставляем в уравнение (***):
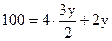
100 = 6y + 2y = 8y
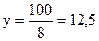
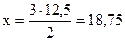
Результаты полученных вычислений можно представить графически (рис. 2.1).
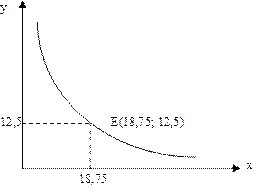
Рис. 2.1
При степенной функции полезности кривая спроса на благо для потребителя может быть получена на основе выражения Лагранжа:
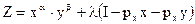



 |


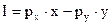
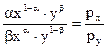



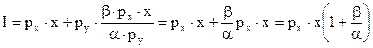

 – функция спроса на благо х
– функция спроса на благо х



 – функция спроса на благо у
– функция спроса на благо у
Вопросы
1. Какой угол наклона у кривых спроса х и у?
2. Являются блага х и у нормальными или низкого качества?
3. Блага х и у являются заменителями или совершенными субститутами?