
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Цены и благосостояние
|
|
Для решения вопроса о приобретении больше чем 2-х благ используется модель, включающая конкретное благо (х) и набор всех других благ (у). Набор благ (у) – это количество денег, израсходованных на все другие товары, называют композиционным товаром или маршалловыми деньгами.
Композиционный товар – часть дохода потребителя, оставшегося после покупки блага х.
Допустим, И(х, y)
I – доход потребителя; px1 – цена блага х; py – цена композиционного товара равна 1.

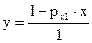

Угловой коэффициент линии бюджетного ограничения – pх1.
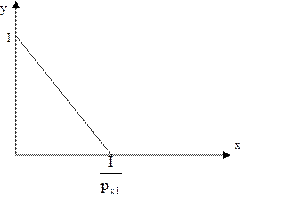
Рис. 4.1
Цена блага х возросла и составила pх2.
Угловой коэффициент линии бюджетного ограничения – pх2.
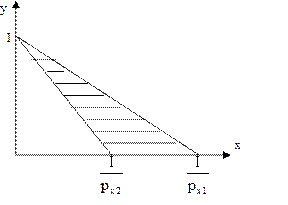
Рис. 4.2
Альтернативные затраты на приобретение блага х возросли (угол наклона увеличился – pх2 > pх1). Благо х становится дороже относительно других благ. Вследствие увеличения цены на благо х для приобретения дополнительной единицы данного блага приходится отказываться от большего количества единиц других благ (у), то есть остается все меньше денег на приобретение этих благ (у).
Потребитель становится беднее, поскольку ему недоступны наборы благ из заштрихованной области (рис. 4.2).
После увеличения цены на благо х доступный набор благ для потребителя лежит на кривой безразличия более низкого порядка. Благосостояние потребителя снизилось. Рис. 4.3 показывает выбор потребителя:
при цене pх1 – точка Е1,
при цене pх2 – точка Е2.
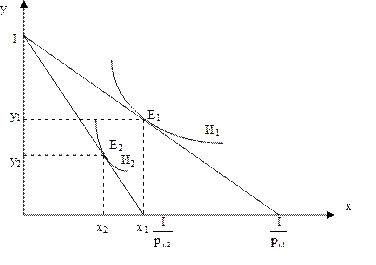
Рис. 4.3
В результате увеличения цены блага х потребление блага х снизилось на ∆ х (х2 – х1). Снизилось потребление и других благ на ∆ у (у2 – у1).
Кривая безразличия И2 находится левее и ниже кривой безразличия И1.
Рассмотрим возможность для потребителя получить первоначальный уровень удовлетворения, т.е. находиться на кривой безразличия И1, но уже после повышения цены на благо х до уровня рх2. В связи с этим потребителю необходимо предоставить некоторую сумму денег. Доход потребителя увеличивается, и он имеет другую бюджетную линию (бюджетное ограничение) –  с углом наклона рх2. Таким образом, потребитель, с одной стороны, находится на кривой безразличия И1, с другой стороны, на другой бюджетной линии
с углом наклона рх2. Таким образом, потребитель, с одной стороны, находится на кривой безразличия И1, с другой стороны, на другой бюджетной линии  , параллельной бюджетной линии
, параллельной бюджетной линии 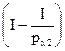 . Рис. 4.4 показывает эффект замещения и эффект дохода для блага х и у в результате роста цены блага х.
. Рис. 4.4 показывает эффект замещения и эффект дохода для блага х и у в результате роста цены блага х.
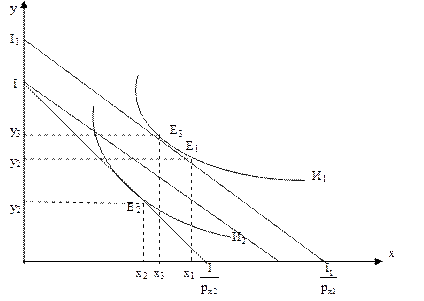 Рис. 4.4
Рис. 4.4
Эффект замещения – движение вдоль кривой безразличия И1 из точки Е1 в точку Е3.
Изменение в объеме спроса на благо х под влиянием эффекта замещения:
х3 – х1
Изменение в объеме спроса на благо х под влиянием эффекта дохода:
х2 – х3
Наблюдаемое изменение объема спроса:
х2 – х1 = Эффект дохода + Эффект замещения
Доход потребителя компенсируется на величину (I1 – I).
Эффект замещения называется компенсированной реакцией на изменение цены (х3 – х1).
Изменение объема спроса на благо х (х2 – х1) называют некомпенсированной реакцией.
На рис. 4.4 реакция потребителя на изменение цены блага х такова, что эффект замещения и эффект дохода снижают объем спроса на благо х. Таким образом, оба эффекта направлены в одну сторону. Это означает, что благо х – нормальное благо, и оно подчиняется закону спроса – функция спроса имеет отрицательный наклон.
В табл. 4.1 представлены возможные варианты влияния повышения цены блага.
Таблица 4.1
Повышение цены блага и его тип
| Тип товара | Эффект замещения | Эффект дохода | Суммарный эффект |
| Нормальный | Объем спроса снижается | Объем спроса снижается | Объем спроса снижается |
| Товар низкого качества (не Гиферена) | Объем спроса снижается | Объем спроса увеличивается | Объем спроса снижается |
| Товар Гиффена | Объем спроса снижается | Объем спроса увеличивается | Объем спроса увеличивается |
На рис. 4.5 показаны две функции спроса потребителя на благо х в результате повышения цены блага х с рх1 до рх2. Функция спроса d1 без компенсации; d2 – с компенсацией.
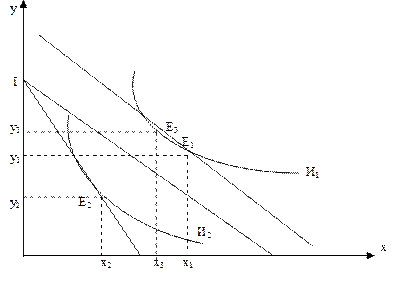
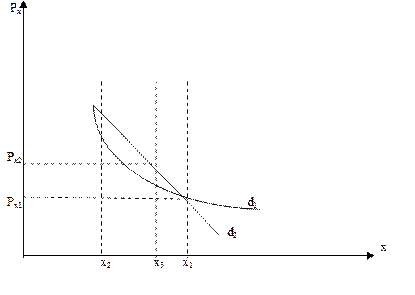
Рис. 4.5
Вопросы
1. Определить угол наклона бюджетной линии в точках Е1, Е2, E3, на рис. 4.5.
2. Определить сумму дотации (компенсированного дохода) на рис. 4.5.
3. Построить график компенсированной реакции для товара низкого качества, но не товара Гиффеана (см. табл. 4.1).
4. Построить график компенсированной реакции для товара Гиффена (см. табл. 4.1).
5. Построить функцию спроса для товара низкого качества, но не товара Гиффена (см. табл. 4.1).
6. Построить функцию спроса на товар Гиффена (см. табл. 4.1).
7. Построить график компенсированной реакции для нормального блога при снижении цены на него.
8. Построить график функции спроса для нормального блага спроса при снижении цены на него.
9. Построить график компенсированной реакции на товар низкого качества (но не товара Гиффена) при снижении цены на него.
10. Построить график функции спроса на товар низкого качества (но не товар Гиффена) на основе пункта 9.
11. Построить график компенсированной реакции на товар Гиффена при снижении цены на него.
12. Построить график функции спроса на товар Гиффена на основе пункта 11.
13. Результаты заданий пунктов 7, 9, 11 представить в таблице (аналогично табл. 4.1).