Функция спроса и эластичность

Категория эластичности пришла в экономику из физики[3], но если в физике понятие эластичности имеет прямой смысл, то в экономике эластичность употребляется не в собственном, а в переносном смысле, т.е. является метафорой.

В экономическую науку этот термин ввёл Альфред Маршалл (1842-1924) для анализа реакции потребителей на изменение цены товара. Впоследствии концепция эластичности получила широкое распространение и нашла применение не только в экономических исследованиях, но и на практике.

Рассмотрим виды эластичности, используемые в теории потребления и спроса.

Эластичность спроса по цене (price elasticity of demand) выражает характер зависимости относительного изменения объема спроса блага при относительных изменениях его цены.

Коэффициент эластичности спроса по цене (иначе, ценовой или прямой эластичности) обозначают как 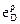– показывает процентное изменение объема спроса на благо при изменении его цены на один процент:

е 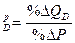, (1)

где - процентное изменение объема спроса на благо;

% - процентное изменение цены блага.

Поскольку коэффициент эластичности – это соотношение относительных приростов, т.е. выражен в процентах, то он не зависит от единиц измерения (тонн, метров, рублей и т.п.).

Задача 1. За прошедший период цена на данный товар выросла на 50%, а объем спроса не него сократился на 25%. Определить эластичность спроса по цене на данный товар.

Решение: е = .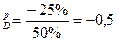

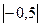Ответ: спрос неэластичный, при росте цены на 1%, объем спроса на благо снизился на 0, 5%.

В соответствии с законом спроса цена и объем реализуемого блага находятся в обратно пропорциональной зависимости (при повышении цены объем спроса сокращается, а при понижении цены увеличивается), поэтому коэффициент эластичности спроса по цене всегда будет иметь отрицательное значение. В экономической практике принято оперировать абсолютным значением этого коэффициента (по модулю), понимая, что в действительности он отрицателен.

Если заменить в формуле (1) % 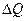на относительное изменение величины объема спрос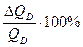а , а

% на относительное изменение цены , то получим:

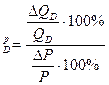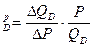е или е (2)

Ценовая эластичность бывает дуговой и точечной.

При расчете коэффициентов дуговой или точечной эластичности формула (2) принимает несколько иной вид. Рассмотрим каждый вид ценовой эластичности подробнее.

Дуговая эластичность. Эластичность спроса по цене будет дуговой, когда коэффициент эластичности определяется по дуге (отрезке) кривой спроса, например, на рис. 3.1. – дуга АВ.

Определим формулу дуговой эластичности спроса по цене, используя формулу (2), в результате получим:

e = .

В правой части формулы (2) вычисляют среднее арифметическое значение координат концов дуги, причем первоначальные значения вычитаются из последующих.

Таким образом, формула дуговой эластичности спроса по цене имеет вид:

е 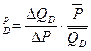(3)

где 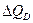- изменение объема спроса на благо;

- изменение цены блага;

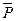- среднее значение цены блага;

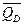- среднее значение объема спроса на благо.

Задача 2. Определить коэффициент эластичности спроса по цене, если известно, что при цене товара 4 руб. за кг (Р = 4 руб.) объем спроса на данный товар 8 кг (Q_D = 8 кг), при повышении цены на 2 руб. ( = 2 руб.) стали покупать на 2 кг меньше (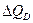 = -2 кг).

Рис. 3.1. Дуговая эластичность

Решение: рассчитаем коэффициент дуговой эластичности спроса по цене по формуле (3):

е

Ответ: спрос неэластичный на отрезке АВ.

Фактически по формуле (3) при расчете коэффициента определяют значение ценовой эластичности в середине отрезка АВ.

Дуговую эластичность спроса по цене применяют тогда, когда имеют дело с большими изменениями цены или с кривой спроса, не являющейся прямой линией.

Более точно эластичность спроса по цене можно рассчитать в любой точке непрерывной функции спроса, т.е. определить точечную эластичность спроса по цене.

Точечная эластичность. Для определения формулы точечной эластичности спроса по цене заменим в формуле (2) 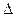-разность на - частную производную и получим формулу:

е (4)

Задача 3. Рассчитать коэффициент точечной эластичности спроса по цене в точках А и В, используя данные задачи 2 и допуская, что функция спроса имеет вид: Q_D = 12 – P.

Рис. 3.2. Точечная эластичность

Решение:

В точке А: Р_А=6, Q_A=6. Дифференцируя функцию Q_D = 12 -P по Р (берем частную производную), получим:

е .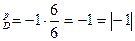

В точке В: при Р_В=4, Q_B=8 ценовая эластичность будет:

е .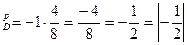

Ответ: в точке А эластичность спроса единичная, а в точке В – спрос неэластичный.