Объект управления

Задание

1. Выбрать произвольный объект управления второго порядка.

2. Описать объект управления и систему управления, в том числе построить функциональную схему системы управления, разработать матмодель объекта управления, привести объект управления к обобщенному виду; выделить из обобщенной модели идеальную модель объекта управления.

3. Для идеальной модели разработать систему релейного управления.

4. Рассчитать и исследовать дискретного систему подчиненного управления с ограничением производной.

5. Исследовать эффективность разработанной системы для исходной модели

объекта управления.

Описание системы управления

Объект управления

В данной работе приведено исследование системы управления мобильным роботом при движении по гладкой поверхности при проскальзывания ведущих колес. В частности, подобный эффект можно наблюдать при разгоне автомобиля на гололеде. В подобных режимах работы тяга привода в первом приближении может быть представлена пропорционально скорости, с которой ведущее колесо перемещается относительно поверхности. Коэффициент вязкого трения, определяющий эту зависимость, в первую очередь, зависит от массы мобильного робота и гладкости поверхности. Объект управления представлен на рисунке 1. На схеме обозначено:

w – угловая скорость вращения ведущего колеса

r – радиус ведущего колеса

x – координата (положение) мобильного робота,

m – масса мобильного робота,

F_T – тяга привода.

Рисунок 1. Мобильный робот.

Параметры мобильного робота и системы управления:

масса: m=10(кг);

максимальная угловая скорость вращения ведущего колеса: ;

радиус колеса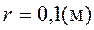

коэффициент вязкого трения между ведущим колесом и поверхностью:

;

время квантования дискретной системы управления: T=0, 01(c).