
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методы изучения взаимосвязей
|
|
Взаимосвязи общественных явлений, их виды и формы.
Методы изучения взаимосвязей
Исследование объективно существующих связей между явлениями – важнейшая задача общей теории статистики. В процессе статистического исследования зависимостей вскрываются причинно-следственные отношения между явлениями, что позволяет выявлять факторы (признаки), оказывающие существенное влияние на вариацию изучаемых явлений и процессов.
Причинно-следственные отношения – это связь явлений и процессов, при которой изменение одного из них (причины) ведет к изменению другого (следствия).
Причина –это совокупность условий, обстоятельств, действие которых приводит к появлению следствия. Если между явлениями действительно существуют причинно-следственные отношения, то эти условия должны обязательно реализовываться вместе с действием причин. Причинные связи носят всеобщий и многообразный характер, и для обнаружения причинно-следственных связей необходимо отбирать отдельные явления и изучать их изолированно.
Особое значение при исследовании причинно-следственных связей имеет выявление временной последовательности: причина всегда должна предшествовать следствию, однако не каждое предшествующее событие следует считать причиной, а последующее – следствием.
Особенностью причинно-следственных связей в социально-экономических явлениях является их транзитивность, т.е. причина Xи следствие У связаны соотношением: Х → Х¢ → Х² → У, а не непосредственно Х → У. Однако промежуточные факторы, как правило, при анализе опускаются.
Социально-экономические явления представляют собой результат одновременного воздействия большого числа причин. Следовательно, при изучении этих явлений необходимо, абстрагируясь от второстепенных, выявлять главные, основные причины.
На первом этапе статистического изучения связи осуществляется качественный анализ изучаемого явления методами экономической теории, социологии, конкретной экономики.
На втором этапе строится модель связи на основе методов статистики: группировок, средних величин, таблиц и т. д.
На третьем этапе интерпретируются результаты, анализ вновь связан с качественными особенностями изучаемого явления.
Статистика разработала множество методов изучения связей, выбор которых зависит от целей исследования и поставленных задач. Связи между признаками и явлениями, ввиду их большого разнообразия, классифицируются по ряду оснований.
Признаки по значению для изучения взаимосвязи делятся на два класса. Признаки, обуславливающие изменения других, связанных с ними признаков, называются факторными, или просто факторами (х). Признаки, изменяющиеся под действием факторных признаков, являются результативными (у).
Различают 3 основных вида статистических взаимосвязей:
1) Балансовые (система показателей, представляющая собой равенство двух частей, состоящих из отдельных элементов). Например:
Начальный остаток + Поступление = Расход + Конечный остаток
2) Компонентные (изменение какого-либо сложного явления полностью определяется изменением компонентов, входящих в это сложное явление как множители). Например:
Стоимость товара = Количество товара х Цена за единицу;
Затраты на производство продукции = Количество продукции х Себестоимость единицы продукции.
3) Факторные (проявляются в согласованной вариации различных признаков у единиц одной и той же совокупности), которые разделяются на:
- Функциональные;
- Стохастические.
Функциональной называют такую связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака, функциональная связь проявляется во всех случаях наблюдения и для каждой конкретной единицы исследуемой совокупности (т.е. это связи полные, жесткие).
Если причинная зависимость проявляется не в каждом отдельном случае, а в общем, среднем при большом числе наблюдений, то такая зависимость называется стохастической (т.е. это связи неполные, соотносительные). Частным случаем стохастической является корреляционная связь, при которой изменение среднего значения результативного признака обусловлено изменением одного или нескольких факторных признаков.
Формы связей:
1) По направлению выделяют связь прямую и обратную.
При прямой связи с увеличением или уменьшением значений факторного признака происходит увеличение или уменьшение значений результативного. Так, например, рост производительности труда способствует увеличению уровня рентабельности производства.
В случае обратной связи значения результативного признака изменяются под воздействием факторного, но в противоположном направлении по сравнению с изменением факторного признака. Так, с увеличением уровня фондоотдачи снижается себестоимость единицы производимой продукции.
2) По аналитическому выражению выделяют связи прямолинейные (или просто линейные) и нелинейные.
Если статистическая связь между явлениями может быть приближенно выражена уравнением прямой линии, то ее называют линейной связью, если же она выражается уравнением какой-либо кривой линии (параболы, гиперболы, степенной, показательной, экспоненциальной и т. д.), то такую связь называют нелинейной, или криволинейной.
3) По количеству факторных признаков различают связи однофакторные и многофакторные.
Если изучается связь между результативным признаком (у) и одним признаком-фактором (х), то данная связь однофакторная.
Многофакторная связь выражает зависимость результативного признака (у) от нескольких признаков-факторов, действующих одновременно, комплексно.
Методы изучения взаимосвязей
Балансовый метод – изучает балансовые связи и заключается в построении балансовых таблиц (характеризует структуру совокупности, позволяет определить искомые показатели из балансовой зависимости, группировать единицы совокупности по различным признакам и т.д.).
Индексный метод – изучает компонентные связи с помощью построения систем взаимосвязанных индексов.
Метод группировок – изучает факторные связи (заключается в разделении всей совокупности на группы по факторному признаку; позволяет выявить наличие связи и ее направление).
Корреляционно-регрессионный метод – изучает факторные (корреляционные) связи.
Регрессионный анализ заключается в определении аналитического выражения связи, т.е. подборе такой формы функциональной связи, которая в наибольшей степени соответствует сущности обнаруженной корреляционной зависимости.
Корреляционный анализ позволяет определить тесноту связи, т.е. с помощью специальных показателей измерить, в какой мере корреляционная связь приближается по своей силе к связи функциональной.
Корреляция – это статистическая зависимость между случайными величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.
В статистике различаются следующие варианты зависимостей:
- Парная корреляция – связь между двумя признаками (результативным и факторным);
- Множественная корреляция – зависимость результативного и двух или более факторных признаков, включенных в исследование;
- Частная корреляция – зависимость между результативным и одним факторным признаком при фиксированном значении других факторных признаков (элиминирование).
Корреляционно-регрессионный анализ проводится в несколько этапов:
1. Выбор типа функции
2. Построение уравнения регрессии
3. Оценка значимости параметров регрессии
4. Измерение тесноты связи
Взаимосвязь двух признаков изображается графически с помощью корреляционного поля (рис. 4.2). В системе координат на оси абсцисс откладываются значения факторного признака (х), на оси ординат – результативного (у). При отсутствии тесных связей наблюдается беспорядочное расположение точек на графике. Чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии.
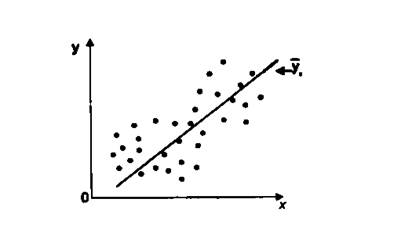
Рис. 4.2. График корреляционного поля
По распределению точек корреляционного поля необходимо подобрать теоретическую функцию, которая будет наилучшим образом выражать зависимость признака Y от фактора X, условно исключая другие факторы: у = ƒ (х).