Построение уравнения регрессии при различных формах связей

Уравнением регрессии называют теоретическую линию связи, а ее построение, анализ и практическое применение – регрессионным анализом. Форму связи определяют прежде всего качественным анализом содержания рассматриваемой зависимости. При построении однофакторной модели известную помощь может оказать рассмотрение графика эмпирической линии регрессии, дающего зрительное представление о направленности и характере связи.

В зависимости от характера изменения результативного признака (у) с изменением факторного признака (х) связи могут быть линейными и нелинейными.

Уравнение линейной связи: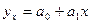

Нелинейные зависимости:

- парабола 2-го порядка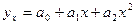

- парабола 3-го порядка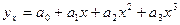

- гипербола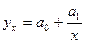

и т. д.

Выбор теоретической формы связи всегда связан с некоторой условностью, вызванной тем, что нужно находить форму функциональной зависимости, в то время как на самом деле зависимость лишь в той или иной степени приближается к функциональной. Но если зависимость довольно высокая (приближена к функциональной), то теоретическая форма связи и ее параметры приобретают большое практическое значение в анализе.

Параметры уравнения регрессии определяют методом наименьших квадратов (МНК), при котором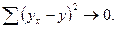

Параметры являются решением системы нормальных уравнений:

для прямой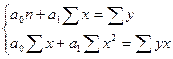

для параболы 2-го порядка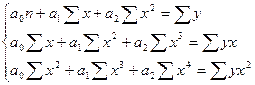

для параболы 3-го порядка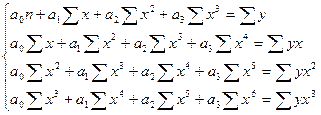

для гиперболы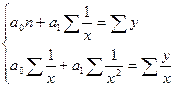

Параметр а₁ при х в уравнении регрессии имеет практическое значение – это коэффициент регрессии, который характеризует, в какой мере увеличивается у_х с ростом на единицу величины х.

Случайная ошибка коэффициента регрессии и его значимость:

,

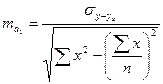где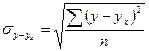

Если фактическое превышение параметра а₁ своей случайной ошибки больше трех 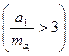, то с большой вероятностью можно считать параметр а₁ не случайным, а значимым.

Количественную зависимость изменения значения у_х от изменения х, которую выражает коэффициент регрессии а₁, часто бывает удобнее выразить в относительных величинах. Для этого вычисляется коэффициент эластичности (Э), который характеризует, на сколько процентов увеличивается у_х при увеличении х на 1%. Коэффициенты эластичности меняют свое значение с изменением величины х.

При многофакторном регрессионном анализе зависимость результативного признака у от факторных признаков х₁, х₂, х₃ … х_n определяется функцией