
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методы сравнения параллельных рядов.
|
|
После того как на основании теоретического анализа будет выявлено, что между изучаемыми признаками возможна взаимосвязь, установить наличие связи и получить представление о ее характере можно с помощью сравнения параллельных рядов. Для этого проводится ранжирование единиц совокупности по факторному признаку (расположение в возрастающем или убывающем порядке – в зависимости от развития процесса и целей исследования). Параллельно записываются значения результативного признака. Путем сопоставления расположенных таким образом рядов значений выявляются наличие связи и ее направление.
На основе сравнения параллельных рядов могут быть рассчитаны элементарные показатели, характеризующие направление и тесноту связи:
Коэффициент Фехнера – оценивает связь на основе сравнения знаков отклонений значений признаков от средних показателей.
Знаки отклонений:
«+», если значение признака больше средней: 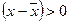 и
и  .
.
«-», если значение признака меньше средней: 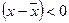 и
и 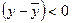 .
.
Совпадение знаков отклонений по обоим признакам означает согласованную вариацию, несовпадение знаков – нарушение согласованности. На этом построен коэффициент Фехнера:
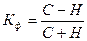 ,
,
где С – число совпадений знаков отклонений;
Н – число несовпадений знаков.
Коэффициент Фехнера изменяется в пределах: - 1 £ Кф £ 1.
Если Кф = 1, то существует согласованная прямая изменчивость.
Если Кф = - 1, то существует согласованная обратная изменчивость.
Если Кф = 0, то согласованная изменчивость отсутствует.
Коэффициент Фехнера улавливает только направление вариации, но не учитывает ее величину, поэтому оценка силы связи получается грубая.
Коэффициент корреляции рангов Спирмена – более точно оценивает силу связи.
Этот коэффициент учитывает согласованность рангов, т.е. порядковых номеров, которые занимают единицы совокупности по каждому признаку:
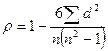 ,
,
где d – разность рангов;
n – число единиц совокупности.
Коэффициент корреляции рангов изменяется в пределах: - 1 £ r £ 1.
При r = 1 – полная прямая корреляция рангов.
При r = - 1 – полная обратная корреляция рангов.
При r = 0 – корреляция рангов отсутствует.
Таким образом, для расчета коэффициента корреляции рангов можно не знать количественных значений признака – достаточно их рангов.
2) Методы однофакторного корреляционного анализа – позволяют с большой точностью определить тесноту связи между факторным признаком (х) и результативным признаком (у) с помощью ряда показателей, расчет которых основан на построении уравнения регрессии или проводится одновременно с регрессионным анализом.
Индекс корреляции (теоретическое корреляционное отношение):
 ,
,
где 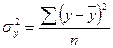 ;
; 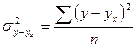 .
.
Индекс корреляции изменяется в пределах: 0 £ R £ 1.
Если R = 0, то связь между вариацией признаков у и х отсутствует.
Если R = 1, то связь между признаками у и х полная, функциональная.
Индекс корреляции используется для измерения тесноты связи при любой ее форме. Выравнивая значение у по разным функциям, по величине дисперсии, характеризующей остаточную вариацию (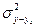 ), можно судить о том, какая функция в наилучшей степени выравнивает эмпирическую линию связи. Однако индекс корреляции не показывает направление связи, а только ее тесноту.
), можно судить о том, какая функция в наилучшей степени выравнивает эмпирическую линию связи. Однако индекс корреляции не показывает направление связи, а только ее тесноту.
Линейный коэффициент корреляции – частный случай общего индекса корреляции, применение которого ограничено только линейной формой связи.
Линейный коэффициент корреляции построен на сопоставлении стандартизованных отклонений варьирующих признаков от их среднего значения.
Исходная формула линейного коэффициента корреляции:
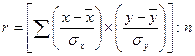 ,
,
где sx и sy – средние квадратические отклонения – соответственно х от 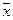 и у от
и у от 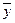 .
.
После преобразования и замены значений 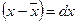 и
и 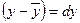 формула будет записана следующим образом:
формула будет записана следующим образом:
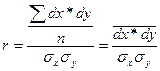 ,
,
т.е. коэффициент корреляции представляет собой частное от деления среднего значения произведений отклонений признаков на произведение их средних квадратических отклонений.
Дальнейшее преобразование приводит формулу к следующему виду, наиболее удобному для вычислений:
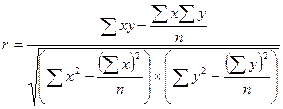 .
.
Из приведенной формулы коэффициента корреляции можно определить коэффициент регрессии, не вычисляя уравнения связи:
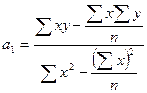 .
.
После дальнейших преобразований формулы линейного коэффициента корреляции получим:
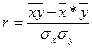 .
.
В отличие от индекса корреляции, линейный коэффициент корреляции показывает не только тесноту, но и направление связи и изменяется в пределах: - 1 £ r £ 1.
При r > 0 связь прямая, при r < 0 связь обратная. Чем ближе значение r к единице, тем теснее связь (т.е. тем она ближе к функциональной зависимости).
Эмпирическое корреляционное отношение – используется для измерения тесноты связи при разделении совокупности на группы (в основном при нелинейной зависимости):
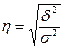 ,
,
где d2 – межгрупповая дисперсия результативного признака;
σ 2 – общая дисперсия результативного признака.
Эмпирическое корреляционное отношение изменяется в пределах: 0 £ h £ 1.
При h = 0 связь отсутствует, при h = 1 связь функциональная.
Для качественной оценки тесноты связи на основе показателя корреляционного отношения можно использовать таблицу:
| Величина показателя | Сила связи |
| 0, 1 – 0, 3 | слабая |
| 0, 3 – 0, 5 | умеренная |
| 0, 5 – 0, 7 | заметная |
| 0, 7 – 0, 9 | тесная |
| 0, 9 – 0, 99 | очень тесная |
Непараметрические методы измерения тесноты связи.
Коэффициент взаимной сопряженности А.А. Чупрова – наиболее общий показатель тесноты связи, применяется для измерения связи двух атрибутивных признаков, когда это изменение образует несколько (3 и более) групп:
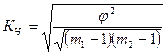 ,
,
где φ 2 – показатель взаимной сопряженности;
m – число групп по каждому признаку.
Расчет показателя взаимной сопряженности производится с помощью таблицы взаимной сопряженности:
| Группы признака А | Группы признака В | Итого | ||
| В1 | В2 | В3 | ||
| А1 | f1 | f2 | f3 | n1 |
| А2 | f4 | f5 | f6 | n2 |
| А3 | f7 | f8 | f9 | n3 |
| Итого | m1 | m2 | m3 | - |
По 1-й строке: 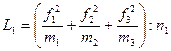
По 2-й строке: 
По 3-й строке: 
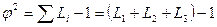
Коэффициент взаимной сопряженности Чупрова изменяется в пределах: 0 < КЧ < 1, но уже при КЧ = 0, 3 можно говорить о тесной связи между вариацией признаков.
Коэффициент взаимной сопряженности Пирсона – применяется для измерения тесноты связи и его использование возможно, когда каждый из качественных признаков состоит более чем из двух групп:
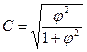
Коэффициент взаимной сопряженности Пирсона изменяется в пределах: 0 < С < 1, чем ближе значение коэффициента к единице, тем теснее связь.
Коэффициенты ассоциации и контингенции – применяются для измерения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп.
Для вычисления коэффициентов строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным, т.е. состоящим из двух качественно отличных друг от друга значений признака:
| a | b | a + b |
| c | d | c + d |
| a + c | b + d | a + b + c + d |
Коэффициент ассоциации: 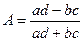
Коэффициент контингенции: 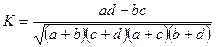
Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной, если А ³ 0, 5 или К ³ 0, 3.