
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Закон распределения вероятностей дискретной случайной величины. На первый взгляд может показаться, что для задания дискретной случайной величины достаточно перечислить все ее возможные значения
|
|
На первый взгляд может показаться, что для задания дискретной случайной величины достаточно перечислить все ее возможные значения. В действительности это не так: случайные величины могут иметь одинаковые перечни возможных значений, а вероятности их – различные. Поэтому для задания дискретной случайной величины недостаточно перечислить все возможные ее значения, нужно еще указать их вероятности.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями
Закон распределения дискретной случайной величины можно задать таблично, аналитически (в виде формулы) и графически.
При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая – их вероятности:
| X | x1 | x2 | … | xn |
| p | p1 | p2 | … | pn |
Приняв во внимание, что в одном испытании случайная величина принимает – одно и только одно возможное значение, заключаем, что события X = х1, X = х2, …, X = хп образуют полную группу; следовательно, сумма вероятностей этих событий, т.е. сумма вероятностей второй строки таблицы, равна единице:
p1 + p2 + …+ pn = 1
Если множество возможных значений X бесконечно (счетно), то сумма ряда p1 +p2 + … равна единице.
Пример 3. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 500 руб. и десять выигрышей по 100 руб. Найти закон распределения случайной величины X – стоимости возможного выигрыша для владельца одного лотерейного билета.
Решение. Напишем возможные значения X: х1= 500, х2 = 100, х3=0. Вероятности этих возможных значений таковы: p1=0, 01; p2 =0, 1; p3=0, 89.
Напишем искомый закон распределения:
| X | |||
| Р | 0, 01 | 0, 1 | 0, 89 |
Контроль: 0, 01 + 0, 1 + 0, 89 = 1.
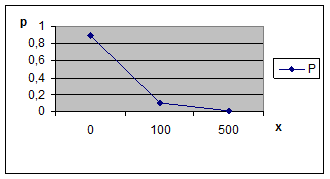 Для наглядности закон распределения дискретной случайной величины можно изобразить и графически, для чего в прямоугольной системе координат строят точки (xi, рi), а затем соединяют их отрезками. Полученную фигуру называют многоугольником распределения.
Для наглядности закон распределения дискретной случайной величины можно изобразить и графически, для чего в прямоугольной системе координат строят точки (xi, рi), а затем соединяют их отрезками. Полученную фигуру называют многоугольником распределения.