Биномиальное распределение. Пусть производится пнезависимых испытаний, в каждом из которых событие А может появиться либо не появиться

Пусть производится п независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна иравна р (следовательно, вероятность непоявления q = 1 – р). Рассмотрим в качестве дискретной случайной величины X число появлений события А в этих испытаниях.

Поставим перед собой задачу: найти закон распределения величины X. Для ее решения требуется определить возможные значения X и их вероятности. Очевидно, событие А в п испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза,..., либо п раз. Таким образом, возможные значения X таковы: х₁=0, х₂=1, х₃=2, …, x _n+1 =n. Остается найти вероятности этих возможных значений, для чего достаточно воспользоваться формулой Бернулли:

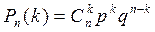, где k = 0, 1, 2,..., п.

Эта запись формулы Бернулли и является аналитическим выражением искомого закона распределения.

Биномиальным называют распределение вероятностей, определяемое формулой Бернулли. Закон назван «биномиальным» потому, что правая часть данного равенства представляет собой разложение так называемого бинома Ньютона:

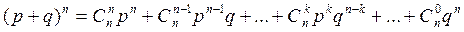
Таким образом, первый элемент разложения рⁿ определяет вероятность наступления рассматриваемого события п раз в п независимых испытаниях; второй элемент np^n-1q определяет вероятность наступления события п - 1 раз; …; последний элемент qⁿ определяет вероятность того, что событие не появится ни разу.

Напишем биномиальный закон в виде таблицы:

X	n	n-1	…	k	…	0
P	рn	npn-1q	…		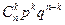…	qn

Пример 4. Монета брошена 2 раза. Написать в виде таблицы закон распределения случайной величины X - числа выпадений «герба».

Решение. Вероятность появления «герба» в каждом бросании монеты р=1/2, следовательно, вероятность непоявления «герба» q = 1 - 1/2 = 1/2.

При двух бросаниях монеты «герб» может появиться либо 2 раза, либо 1 раз, либо совсем не появиться. Таким образом, возможные значения X таковы: х₁=2, х₂=1, х₃=0. Найдем вероятности этих возможных значений по формуле Бернулли:

;

;

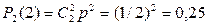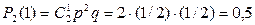
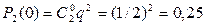Напишем искомый закон распределения:

Контроль: 0, 25 + 0, 5 + 0, 25 = 1.