Распределение Пуассона. Пусть производится пнезависимых испытаний, в каждом из которых вероятность появления события Аравна р

Пусть производится п независимых испытаний, в каждом из которых вероятность появления события А равна р. Для определения вероятности k появлений события в этих испытаниях используют формулу Бернулли. Если же n велико, то пользуются асимптотической формулой Лапласа. Однако эта формула непригодна, если вероятность события мала (p≤ 0, 1). В этих случаях (n велико, р мало) прибегают к асимптотической формуле Пуассона, которая выражается формулой.

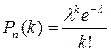
Формула Пуассона позволяет найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно k раз, причем делается допущение, что произведение пр сохраняет постоянное значение, а именно пр = λ.

Замечание. Имеются специальные таблицы, пользуясь которыми можно найти P_n(k), зная k и λ.

Пример 5. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равно 0, 0002. Найти вероятность того, что на базу прибудут 3 негодных изделия.

Решение. По условию, n = 5000, р = 0, 0002, k=3. Найдем λ

λ = пр = 5000*0, 0002 = 1.

По формуле Пуассона искомая вероятность приближенно равна