
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
III. Выводы по результатам выполнения лабораторной работы.
|
|
Задача 1. Установление наличия стохастической связи между факторным признаком Х и результативным признаком Y:
а) графическим методом.
Вывод: На основе анализа диаграммы рассеяния из Лабораторной работы №1, полученной после удаления аномальных значений, можно сделать вывод, что имеет место стохастическая связь. Предположительный вид связи: линейная прямая.
б) методом сопоставления параллельных рядов.
Вывод: Табл.2.1, полученная путем ранжирования предприятий по возрастанию значения факторного признака Х, показывает, что с увеличением значений факторного признака увеличиваются значения результативного признака, за исключением некоторых отклонений, что позволяет сделать вывод о прямой зависимости между среднегодовой стоимостью ОПФ и выпуском продукции.
Задача 2. Установление наличия корреляционной связи между признаками Х и Y методом аналитической группировки.
Вывод: Результаты выполнения аналитической группировки предприятий по факторному признаку Среднегодовая стоимость основных производственных фондов даны в табл. 2.2 Рабочего файла, которая показывает, что с увеличением среднегодовой стоимости основных производственных фондов возрастает выпуск продукции, что говорит о наличии прямой корреляционной зависимости.
Задача 3. Оценка тесноты связи признаков Х и Y:
а) на основе эмпирического корреляционного отношения
Для анализа тесноты связи между факторным и результативным признаками, рассчитывается показатель η - эмпирическое корреляционное отношение, задаваемое формулой
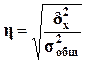
Для вычисления η необходимо знать общую дисперсию 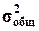 и межгрупповую дисперсию
и межгрупповую дисперсию 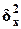 результативного признака Y - Выпуск продукции.
результативного признака Y - Выпуск продукции.
Результаты выполненных расчетов представляются табл. 2.4 Рабочего файла.
Вывод: Величина η = 0, 90 является близкой к единице. Вариация выпуска продукции на 90% обусловлена вариацией стоимости ОПФ. Между этими признаками существует тесная связь.
б) на основе линейного коэффициента корреляции признаков
В предположении, что связь между факторным и результативным признаком имеется, для определения тесноты связи на основе линейного коэффициента корреляции r был использован инструмент Корреляция надстройки Пакет анализа.
Результатом работы инструмента Корреляции является табл. 2.5 Рабочего файла.
Вывод: Значение коэффициента корреляции r = 0, 913188 лежит в интервале 0, 9-0, 99, что в соответствии со шкалой Чэддока, говорит о весьма высокой связи между признаками.
Так как значение коэффициента корреляции r положительное, то связь между признаками прямолинейная.
Посредством показателя η измеряется теснота связи любой формы, а с помощью коэффициента корреляции r – только прямолинейная, следовательно, значения η и r совпадают только при наличии прямолинейной связи. В теории статистики установлено, что если 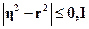 , то гипотезу о прямолинейной связи можно считать подтвержденной.
, то гипотезу о прямолинейной связи можно считать подтвержденной.
Вывод: 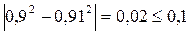 следовательно, между среднегодовой стоимостью основных производственных фондов и выпуском продукции существует тесная связь.
следовательно, между среднегодовой стоимостью основных производственных фондов и выпуском продукции существует тесная связь.
Задача 4. Построение однофакторной линейной регрессионной модели связи изучаемых признаков с помощью инструмента Регрессия надстройки Пакет анализа.
Построение регрессионной модели заключается в определении аналитического выражения связи между факторным признаком X и результативным признаком Y.
Инструмент Регрессия производит расчет параметров а0 и а1 уравнения однофакторной линейной регрессии  и проверка его адекватности исследуемым фактическим данным.
и проверка его адекватности исследуемым фактическим данным.
В результате работы инструмента Регрессия были получены результативные таблицы 2.6 – 2.9 Рабочего файла.
Вывод: Однофакторная линейная регрессионная модель связи факторного и результативного признаков имеет вид y= -375, 44+ 1, 09 х
Доверительные интервалы коэффициентов уравнения регрессии представим в нижеследующей таблице
| Коэффициенты | Границы доверительных интервалов | |||
| С надежностью Р=0, 68 | С надежностью Р=0, 95 | |||
| Нижние | Верхние | Нижние | Верхние | |
| а0 | -841, 28 | 90, 39 | -607, 14 | -143, 75 |
| а1 | 0, 90 | 1, 28 | 0, 9957 | 1, 18 |
С увеличением надежности границы доверительных интервалов сокращаются пределы границ доверительных интервалов.
Экономическая интерпретация коэффициента регрессии а1: При изменении среднегодовой стоимости ОПФ на единицу выпуск продукции меняется возрастает на 9%.
Коэффициент эластичности 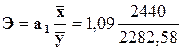 =1, 164481753
=1, 164481753
Экономическая интерпретация коэффициента эластичности Э: при изменении среднегодовой стоимости ОПФ на 1% выпуск продукции возрастает на 16%.
Задача 5. Нахождение наиболее адекватного уравнения регрессии с помощью средств инструмента Мастер диаграмм. Построение для этого уравнения теоретической линии регрессии.
Возможности инструмента Мастер диаграмм позволяют быстро производить построение и анализ адекватности регрессионных моделей, базирующихся на использовании различных видов зависимости между признаками X и Y.
Построение моделей осуществляется непосредственно на диаграмме рассеяния.
На диаграмме рассеяния отображается линия и уравнение регрессии, а также коэффициент детерминации R2.
В лабораторной работе уравнения регрессии и их графики были построены для 5-ти видов зависимости между признаками и даны на диаграмме рассеяния Рабочего файла.
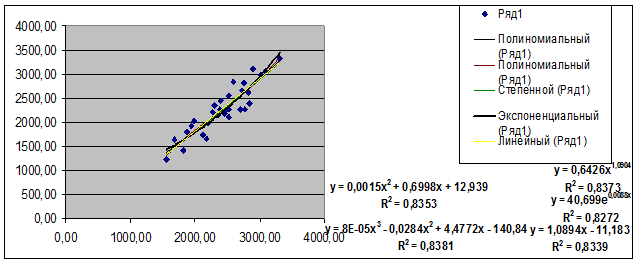
Уравнения регрессии и соответствующие им коэффициент детерминации R2 даны в следующей таблице: