Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Регрессионные модели связи
|
|
| Вид уравнения | Уравнение регрессии | Коэффициент детерминации R2 |
| Линейное | y = 1, 0894x2 - 11, 183 | 0, 8339 |
| Полином 2-го порядка | y = 0, 0015x2 + 0, 6998x + 12, 939 | 0, 8353 |
| Полином 3-го порядка | y = 8E-05x3 - 0, 0284x2 + 4, 4772x - 140, 84 | 0, 8381 |
| Степенное | y = 0, 6426x1, 0904 | 0, 8373 |
| Экспоненциальное | y = 40, 699e0, 0088x | 0, 8272 |
Выбор наиболее адекватного уравнения регрессии определяется максимальным значением коэффициента детерминации R2: чем ближе значение R2 к единице, тем более точно регрессионная модель соответствует фактическим данным
Вывод: Максимальное значение коэффициента детерминации R2 =0, 8381
Вид искомого уравнения регрессии – y = 8E-05x3 - 0, 0284x2 + 4, 4772x - 140, 84
Это уравнение регрессии и его график приведены на отдельной диаграмме рассеяния Рабочего файла.
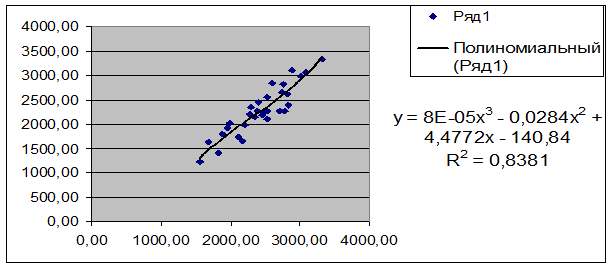
Вместе с тем, так как значения коэффициентов R2 кубического и линейного уравнения расходятся очень незначительно (на величину 0, 0042), а для показателей тесноты связи имеет место неравенство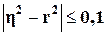 
, то в качестве адекватного уравнения регрессии может быть принято линейное уравнение y = 1, 0894x2 - 11, 183, не совпадающее с найденным с помощью инструмента Регрессия надстройки Пакет анализа.