
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Измерительных приборов и преобразователей
|
|
При проведении измерения какой-либо физической величины исполь-зуются приборы и передаточные элементы, которые совместно и образуют измерительное устройство (средство измерений). Такое измерительное уст-ройство можно условно представить в виде функциональной схемы (рис. 3.2, а), причем каждый из показанных на схеме узлов может представлять собой либо измерительный преобразователь, либо передаточный элемент,
а то и самостоятельное измерительное устройство.
С точки зрения системного анализа вся измерительная установка или измерительная цепь (подобные тем, что показаны на схеме рис. 3.2, а), так же как и её отдельные блоки, функционально одинаковы: на вход подается сигнал измеряемой величины qi, а после преобразований и обра-ботки на её выходе появляется сигнал Qi, причем обе эти величины связаны друг с другом определенными соотношениями, характеризующими данную измерительную систему. Эти соотношения называются передаточ-ными характеристиками. Таким образом, между выходным Qi и входным qi сигналами существует функциональная зависимость (рис. 3.2, б)
Qi = П(qi), (3.1)
где П – передаточная функция.
|
|
|
|

 величина
величина
А
|

 Рис.3.2. Обобщенная модель измерительного устройства:
Рис.3.2. Обобщенная модель измерительного устройства:
qi Qi = П(qi) а – функциональная схема;
б – к понятию “передаточной функции”
б измерительного устройства
Такая функциональная зависимость для измерительной системы должна быть однозначной, т. е. при возрастании либо убывании измеря-емой величины зависимость П(qi) должна оставаться неизменной, при этом стационарное состояние измерительного устройства (или отдельного элемента) достигается, когда заканчиваются все переходные процессы после подачи на вход сигнала qi = const. В этом случае говорят о стати-ческих передаточных характеристиках, а погрешности СИ с такими пере-даточными характеристиками должны описываться в виде некоего стацио-нарного процесса.
Если входная величина qi(t) быстро (или относительно быстро) меняется со временем, то выходная величина Qi (t) может содержать искажения, ко-торые вносят определенный вклад в суммарную погрешность измери-тельной системы (или её отдельного элемента). Источники погрешности СИ в данном случае описываются в виде нестационарных процессов, а передаточная функция представляет собой динамическую передаточную характеристику.
Следует отметить, что физические процессы, происходящие в реальных измерительных приборах, датчиках, измерительных усилителях и прочих измерительных преобразователях, входящих в состав конкретных СИ, характеризуются зависимостью своих параметров от времени (флуктуации, шумы и т. д.). Поскольку эти изменения могут протекать одновременно, то и погрешности СИ, связанные с ними, представляют собой многомерный случайный процесс. Следовательно, общей моделью погрешности является многомерный нестационарный случайный процесс. И лишь как частные случаи могут существовать СИ с погрешностями, описываемыми стацио-нарными (вернее квазистационарными) процессами.
В общем случае анализ случайных процессов достигается при условии эргодичности этих процессов. Стационарный случайный процесс называется эргодическим, если усреднение любой его вероятностной характеристики по множеству реализаций эквивалентно усреднению по времени одной те-оретически бесконечно длинной (т. е. Т→ ∞) реализации [10].
Таким образом для эргодического случайного процесса имеем:
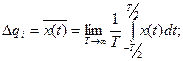 (3.2)
(3.2)
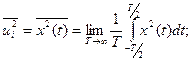 (3.3)
(3.3)
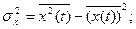 (3.4)
(3.4)
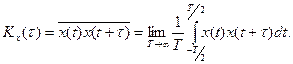 (3.5)
(3.5)
Если х(t) электрический сигнал, то 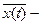 постоянная составляющая погреш-ности этого случайного сигнала,
постоянная составляющая погреш-ности этого случайного сигнала, 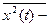 средняя мощность,
средняя мощность, 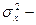 флуктуация сигнала. В выражении (3.5)
флуктуация сигнала. В выражении (3.5) 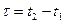 – интервал между моментами t2 и t1 (см. рис. 3.3),
– интервал между моментами t2 и t1 (см. рис. 3.3), 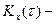 корреляционная функция.
корреляционная функция.
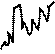
Следует отметить, что физическая природа различных шумов отлична, но структура шумовых сигналов весьма схожа – такие сигналы можно пред-ставить как последовательность дискретных импульсов, случайно распре-деленных во времени (рис. 3.3, б).
 | |||
 | |||
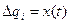



 S Δ х б
S Δ х б
 |



 х
х
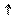

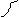


 а
а
τ i U
 | |||
 |
t1 t2 T t
Рис. 3.3. Представление погрешности 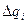 в виде случайного эргодического процесса (а);
в виде случайного эргодического процесса (а);
сильно увеличенная часть сигнала, раскрывающая его дискретную структуру (б).