Билет 13. 1) Гомогенное образование зародышей новой фазы при кристаллизации: причины гомогенного зародышеобразования

1) Гомогенное образование зародышей новой фазы при кристаллизации: причины гомогенного зародышеобразования, механизм и энергия активации процесса, изменение свободной энергии при зародышеобразовании, критический размер зародышей новой фазы, дозародыши и истинные зародыши.

Гомогенное зародышеобразование происходит в гомогенной жидкой фазе, не имеющей внутри себя никаких поверхностей раздела. В микрообъемах расплава возникают образования с более упорядоченной структурой, но не достигающие упорядоченности кристалла. Их размер ~ 4-6 ангстрем. Образование таких зародышей носит статистический характер. Они возникают за счет флуктуаций – мгновенного отклонения свойств микрообъема от всей жидкости. Движение атомов в расплаве – интенсивное. Зародыши которые распадаются – дозародыши. Не распавшиеся зародыши называются истинными. Все определяется свободной энергией:

- если она увеличивается, то образование термодинамически не выгодно – распад зародыша.

- если Δ G< 0, зародыши устойчивы (истинные).

Причины изменения Δ G

- образование границы раздела фаз. На ее образование требуется энергия.

G_s = 4π r² Δ f_s, - за счет образование поверхности раздела.

r – радиус зародыша

Δ f_s – изменение энергии Гиббса на единицу площади. Всегда больше 0.

- связь с образованием более упорядоченной структуры (уменьшение внутренней энергии). G_v = 4/3π r³ Δ f_v,

Δ f_s – изменение энергии Гиббса на единицу объема (меньше 0);

Свободная энергия активации процесса гомогенного зародышеобразования:

Δ G’ = G_s – G_v = 4π r² Δ f_s – 4/3π r³ Δ f_v

При малых значениях r – преобладает G_s.

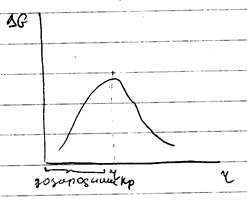
Критический размер соответствует равенству G_s и G_v

Б.№13

2. Правило фаз Гиббса. Вид уравнения правила фаз для тугоплавких силикатных систем. Понятия: фаза, независимый компонент, степени свободы, вариантность системы, равновесное состояние.

Правило фаз Гиббса представляет собой математическую зависимость между числом степеней свобода (F), числом фаз (Р) и числом независимых компонентов (К) в системах, находящихся в равновесном состоянии. В общей форме правило фаз имеет вид:

F + р = k + m

m – число внешних параметров, влияющих на равновесие.

Фазой (Р) называется однородная часть системы с одинаковыми физическими, химическими и термодинамическими свойствами» которая отделена поверхностью раздела от других частей системы (от других фаз) и которую можно выделить из системы механическими средствами.

Под компонентами системы в общем смысле этого слова обычно понимают все те индивидуальные химические соединения, которые существуют в данной системе. Числом независимых компонентов называется минимальное число компонентов (соединений), с помощью которых, используя стехиометрические уравнения, можно выразись состав любой фазы системы.

Число независимых компонентов находится из выражения:

К = Коб - х, где Кобщ - общее число компонентов (соединений), а х - число стехиометрических уравнений реакций, которыми могут быть связаны все компоненты системы.

Например, в системе, состоящей из трех фаз: CaCO3, СaO и CO2, общее число компонентов (соединений) равно трем, однако число независимых компонентов К = 2, поскольку три указанных соединения могут быть связаны одним уравнением реакции СаСО3= СаО + СO2 (процесс разложения СаСO3), т.е. К = 3 - I = 2

Степень свободы (F) – независимые параметры системы, которые можно в определенных пределах изменять, не нарушая равновесия в системе, т.е. не изменяя числа и природы фаз.

Вариантность системы: система, которая не имеет степеней свободы называется инвариантной; с одной степенью свободы – моновариантная; с двумя – дивариантная и т.д.

Для систем, равновесие в которых зависит от давления: F=K-p+2; 2 учитывает температуру и давление.

Для систем с постоянными давлением: F=K-p+1.

Равновесное состояние: признаки: система в равновесном состоянии имеет минимальную энергию Гиббса; одинаковость параметров во всех точках системы; в равновесной системе число и природа фаз не изменяется в определенном интервале параметров.