
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Если количество перчинок N велико, а отношение мало, то задача описывается распределением Пуассона.
|
|
Если количество перчинок N велико, а отношение 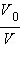 мало, то задача описывается распределением Пуассона.
мало, то задача описывается распределением Пуассона.
В среднем, в ложке должны оказаться 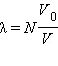 перчинок. Вероятность того, что в ложке окажется ровно n перчинок, равна
перчинок. Вероятность того, что в ложке окажется ровно n перчинок, равна  В частности, при V = 10 л,
В частности, при V = 10 л, 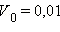 л, N = 50 получаем
л, N = 50 получаем  (то есть одна перчинка, в среднем, попадается на 20 ложек), а вероятность:
(то есть одна перчинка, в среднем, попадается на 20 ложек), а вероятность:
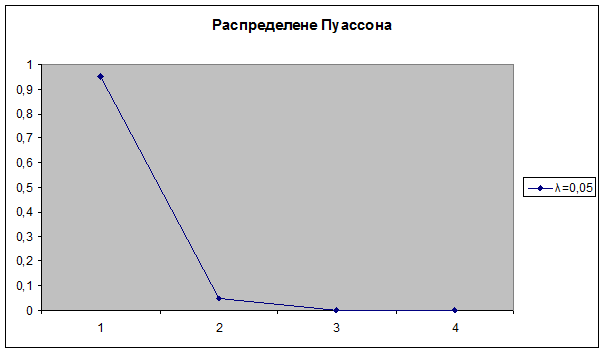
- того, что в ложке окажется ноль перчинок, p 0 ≈ 0, 95123,
- того, что в ложке окажется одна перчинка, p 1 ≈ 0, 04756,
- того, что в ложке окажется две перчинки, p 2 ≈ 0, 00119,
- того, что в ложке окажется три перчинки, p 3 ≈ 0, 00002.
Как видим, pn очень быстро уменьшается с ростом n.
4) Геометрическое распределение. Дискретная случайная величина X имеет геометрическое распределение, если она принимает значения 1, 2,..., m,... (бесконечное, но счётное множество значений) с вероятностями
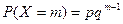
где 0 < p < 1, q=1 - p, m =1, 2,...
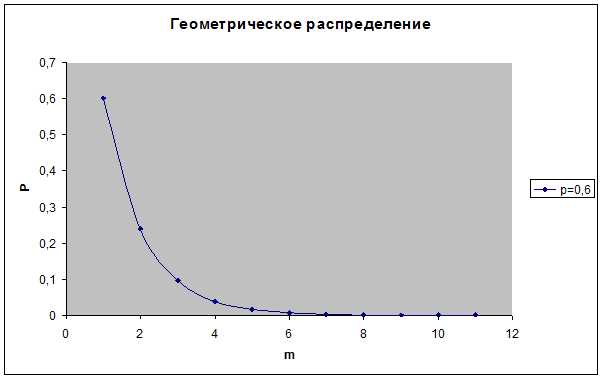
Пример геометрического распределения представлен на рисунке
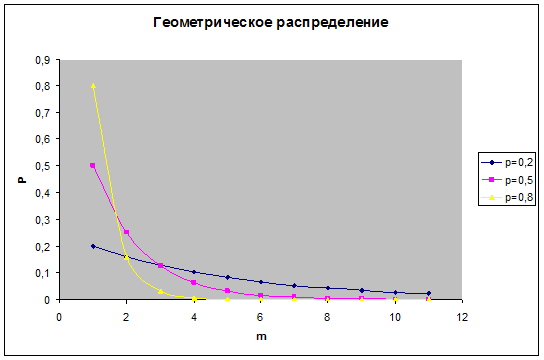
Ряд геометрического распределения имеет вид:
| xi | ... | m | ... | |||
| pi | p | pq | pq 2 | ... | pq m-1 | ... |
Очевидно, что вероятности pi образуют геометрическую прогрессию с первым членом p и знаменателем q (отсюда и название " геометрическое распределение").
Определение геометрического распределения корректно, так как сумма ряда

(так как 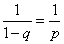 есть сумма геометрического ряда
есть сумма геометрического ряда  при
при 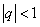 ).
).
Случайная величина X=m, имеющая геометрическое распределение, представляет собой число m испытаний, проведённых по схеме Бернулли, с вероятностью p наступления события в каждом испытании до первого положительного исхода.
Математическое ожидание СВ X, имеющей геометрическое распределение с параметром p, 
Дисперсия  , где q= 1-p.
, где q= 1-p.
Пример. Вероятность поражения цели равна 0, 6. Производится стрельба по мишени до первого попадания (число патронов не ограничено). Требуется составить ряд распределения числа сделанных выстрелов, найти математическое ожидание и дисперсию этой случайной величины. Определить вероятность того, что для поражения цели потребуется не более трёх патронов.
Решение. Случайная величина X - число сделанных выстрелов - имеет геометрическое распределение с параметром p= 0, 6. Ряд распределения X имеет вид:
| xi | ... | m | ... | |||
| pi | 0, 6 | 0, 24 | 0, 096 | ... | 0, 6·0, 4 m | ... |
По формулам 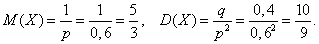
Вероятность того, что для поражения цели потребуется не более трёх патронов равна
P(X≤ 3)=P(X= 1 )+P(X=2)+P(X=3)= 0, 6+0, 24+0, 096=0, 936.