Методы определения угловых коэффициентов излучения

Угловой коэффициент излучения является основной расчетной величиной. Он может быть найден аналитическим, графоаналитическим методом и методом поточной алгебры. К экспериментальным методам относятся методы светового моделирования и методы аналогий.

Аналитический метод. Основан на непосредственном интегрировании математического выражения для элементарного углового коэффициента излучения

.

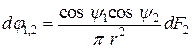Величины, входящие в это выражение, равны

r²=h²+1+R²+2R cos α;

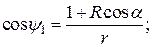
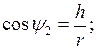dF₂=RdRd .

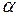Подставляя эти значения в выражение для элементарного углового коэффициента, получаем:

.

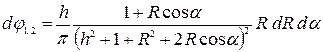Таким образом, аналитический метод связан с операциями по непосредственному интегрированию зависимости, которая является математическим описанием углового коэффициента.

Графоаналитический метод (метод проекций). В этом методе операции интегрирования заменяются графическим проектированием. На полусфере контур лучей, падающих с площадки dF₁ на поверхность второго тела, вырежет площадку 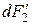, проекция которой выразится площадкой .

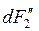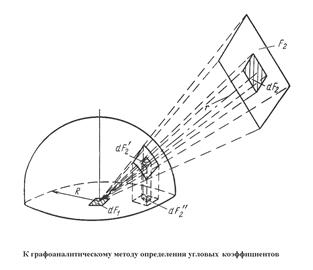Тогда местный угловой коэффициент излучения 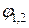равен частному от отделения площадки 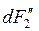на площадь круга радиусом R. Элементарный угловой коэффициент излучения

,

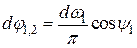Произведение 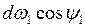является проекцией элементарного угла 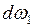, на плоскость, в которой находится площадка dF₁.

Проинтегрировав это выражение, получим значение местного углового коэффициента .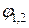

Метод поточной алгебры. В этом методе интегрирование заменяется простыми алгебраическими операциями. В основе метода лежат геометрические свойства лучистых потоков.

Найдем средние значения взаимных поверхностей и угловых коэффициентов излучения для тел с поверхностями F₁ и F₂. Согласно свойству замыкаемости

,

,

.

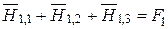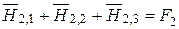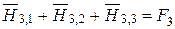Так как, самооблучения не происходит .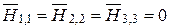

Следовательно, .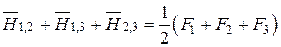

Вычтем последовательно из последнего уравнения, уравнения системы, получим

; ; .

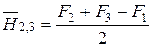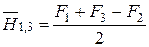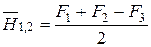С учетом 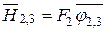, имеем .

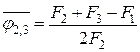По свойству взаимности 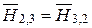; 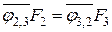, следовательно

.

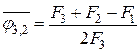Из 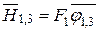имеем 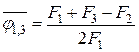. Аналогично

.

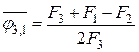Для двух других угловых коэффициентов

.

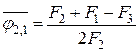
Применительно к сложным геометрическим системам различные криволинейные контуры поперечных сечений заменяются более простыми контурами минимальной длины (натянутыми нитями). Это находится в полном соответствии со свойством совмещаемости лучистых потоков.

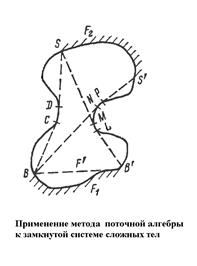Этим методом чаще определяют среднее значение взаимных поверхностей.

Средняя взаимная поверхность излучения равна полусумме внутренних пересекающихся нитей, натянутых между концами контуров, за вычетом полусуммы внешних не пересекающихся нитей

.

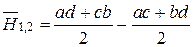Рассмотрим систему пластин одинаковой ширины с относительно большими продольными размерами. Задана ширина а и расстояние междупластинами h. Требуется определить Н_{1, 2} и 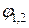. Введем условные поверхности с контурами АС и ВD. Получаем замкнутую систему, состоящую из четырех тел. Свойство замкнутости выразится

,

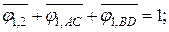
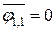откуда искомое значение

.

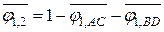Согласно

; ,

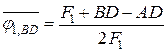где АВ=а; АС=BD=h; AD=BC = .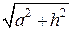

После подстановки этих величин найдем искомое значение среднего углового коэффициента и взаимной поверхности излучения

;

.

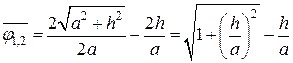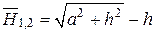Используя метод натянутых нитей можно сразу получить

.

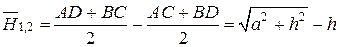Метод светового моделирования. В опытном исследовании углового коэффициента излучения лучистые потоки заменяются световыми, так как оба вида относятся к электромагнитному излучению. Однако световое моделирование обладает рядом преимуществ. В нем устраняются трудности, связанные с измерением лучистых потоков, особенно в области высоких температур.

Метод электрического моделирования. Метод электрического моделирования использовался выше применительно к процессам теплопроводности. Существует также аналогия между переносом энергии излучением заряда в электрической цепи. Результирующий лучистый поток

.

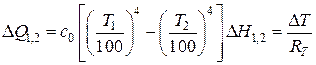С другой стороны

.

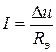Формальное сходство уравнений позволяет измерить потоки излучения и провести опытное исследование угловых коэффициентов излучения.

Вопросы к теме 15.

1. Какие задачи относятся к прямым и обратным?

2. Какие методы исследования лучистого теплообмена знаете? Охарактеризуйте каждый.

3. Как определить тепловой поток излучением в системе плоскопараллельных поверхностей без экранов?

4. Как определить приведенную излучательную способность и приведенный коэффициент поглощения в системе плоскопараллельных поверхностей без экранов?

5. Как влияет наличие экранов на плотность результирующего потока излучения?

6. Что такое излучательная способность твердых тел? Какие методы ее определения знаете?

7. Запишите выражение результирующего потока излучения при теплообмене между телом и его оболочкой.

8. Запишите выражение приведённой излучательной способности такой системы без экранов.

9. Как определить результирующий тепловой поток при теплообмене между телом и его оболочкой для случая 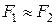и F₁ < < F₂?

10. Теплообмен между телом и его оболочкой при наличии экранов.

11. Особенности теплообмена излучением между телами произвольно расположенными в пространстве.

12. Раскройте понятие элементарного, местного и среднего углового коэффициента.

13. Что называют взаимной поверхностью излучения?

14. Какие свойства лучистых потоков знаете? В чем заключается каждое из них?

15. Какие существуют методы определения угловых коэффициентов? Объясните на каких принципах основан каждый из них.