Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Графическое моделирование дискретной случайной величины
|
|
Моделирование случайной величины
Основы моделирования
Моделирование случайной величины (статистическое моделирование, метод Монте-Карло) является удобным способом теоретического имитирования случайных процессов.
Метод заключается в воспроизведении исследуемого процесса при помощи вероятностной математической модели (процедуры) и вычислении характеристик смоделированного процесса.
Моделирование основано на применении равномерно распределенных случайных чисел (таблица, ЭВМ, алгебраические алгоритмы).
Различают графический и аналитический способы моделирования.
При табличном способе для обеспечения большей случайности каждый раз при моделировании используют некоторую выборку, применяя разные заранее заданные алгоритмы выбора чисел из таблицы (например, подряд, начиная с некоторого по порядку числа, через одно, по строкам или столбцам, вперед или назад, в шахматном порядке и т.д.).
Графическое моделирование дискретной случайной величины
Имеется 10 карточек. На одной имеется надпись 1, на 2-х – 2, на 3-х – 3 и на 4-х – 4. Испытание заключается в извлечении одной карточки из десяти. Затем карточка возвращается назад. Таким образом, имеется случайная величина X, возможные значения которой равны 1, 2, 3 и 4. Можно представить распределение рассматриваемой случайной величины в табличной форме
| X | ||||
| P | 0, 1 | 0, 2 | 0, 3 | 0, 4 |
Математическое ожидание случайной величины mX = 3.
Определим накопленные вероятности случайной величины 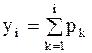 и составим таблицу.
и составим таблицу.
| i | ||||
| xi | ||||
| pi | 0, 1 | 0, 2 | 0, 3 | 0, 4 |
| yi | 0, 1 | 0, 3 | 0, 6 | 1, 0 |
По данным таблицы строим кусочно-линейный график зависимости yi от xi.


Из таблицы случайных чисел по заданному алгоритму выбирается необходимое количество чисел yj, на основе которых осуществляется переход к моделируемой случайной величине X.
| j | … | ||||||||||
| yj | 0, 27 | 0, 03 | 0, 80 | 0, 10 | 0, 54 | 0, 76 | 0, 54 | 0, 76 | 0, 54 | 0, 21 | |
| xj | |||||||||||
| Sj | |||||||||||
| `xj | 2, 0 | 1, 5 | 2, 3 | 2, 0 | 2, 2 | 3, 5 | 2, 7 | 2, 8 | 2, 8 | 2, 7 |
В таблице принято:  ,
,  .
.
По данным таблицы строим график зависимости `xj от j, который асимптотически приближается к линии уровня 3, являющейся математическим ожиданием случайной величины.
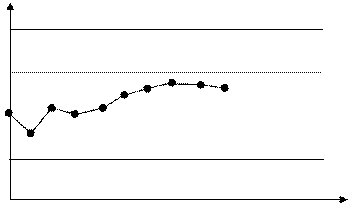 `x j
1 2 3 4 5 6 7 8 9 10 … j `x j
1 2 3 4 5 6 7 8 9 10 … j
|
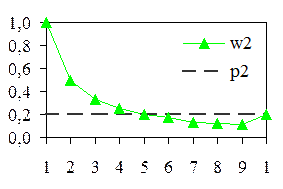
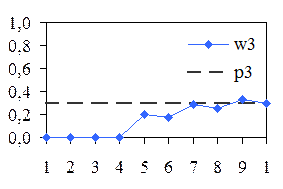
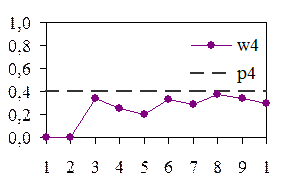
По результатам моделирования определяем относительные частоты.
| j | … | ||||||||||
| xj | |||||||||||
| w1 | |||||||||||
| 0, 5 | 0, 33 | 0, 5 | 0, 4 | 0, 33 | 0, 29 | 0, 25 | 0, 22 | 0, 2 | |||
| w2 | 1, 0 | 0, 5 | 0, 33 | 0, 25 | 0, 2 | 0, 17 | 0, 13 | 0, 125 | 0, 11 | 0, 2 | |
| w3 | 0, 2 | 0, 17 | 0, 29 | 0, 25 | 0, 33 | 0, 3 | |||||
| w4 | 0, 34 | 0, 25 | 0, 2 | 0, 33 | 0, 29 | 0, 375 | 0, 34 | 0, 3 |