Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Аналитическое моделирование непрерывной случайной величины
|
|
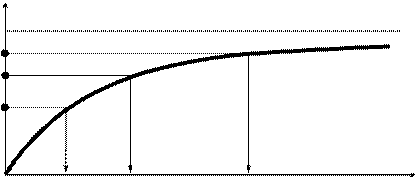
Для моделирования непрерывных случайных величин так же, может быть применен графический способ. Алгоритм в этом случае ничем не отличается от алгоритма моделирования дискретной случайной величины. Но график функции (интегральной) будет уже иметь не кусочно-линейный вид, а представлять непрерывную кривую.
y = F(x) y1 y3 y2
x 0 х2 х3 х1 |
Более удобным является аналитический способ моделирования, применяемый в случаях, когда интегральная функция разрешается в конечном виде.
Рассмотрим аналитический способ моделирования случайной величины, распределенной по показательному закону.
Для данного распределения интегральная функция имеет вид
 ,
,
где l – параметр закона распределения.
Логарифмируя и разрешая равенство относительно x, получим
 .
.
Поскольку y при моделировании – это равномерно распределенная случайная величина, заключенная в интервале от 0 до 1, то (1–y) – тоже равномерно распределенная случайная величина, заключенная в том же интервале. Поэтому, с учетом упрощения, можно также написать следующее выражение для статистического моделирования данной случайной величины, распределенной по показательному закону:
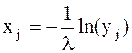 ,
,
где yj – равномерно распределенные случайные числа (0 £ yj £ 1).
В качестве примера рассмотрим моделирование показательно распределенной случайной величины X с параметром l = 0, 8. Математическое ожидание случайной величины при таком законе распределения: mX = 1, 25.
Из таблицы случайных чисел выбирается необходимое количество чисел yj, на основе которых осуществляется переход к моделируемой случайной величине.
| j | … | ||||||||||
| yj | 0, 76 | 0, 54 | 0, 21 | 0, 87 | 0, 12 | 0, 48 | 0, 51 | 0, 18 | 0, 80 | 0, 08 | |
| xj | 0, 343 | 0, 770 | 1, 951 | 0, 174 | 2, 650 | 0, 917 | 0, 842 | 2, 143 | 0, 279 | 3, 157 | |
| Sj | 0, 343 | 1, 113 | 3, 064 | 3, 238 | 5, 888 | 6, 806 | 7, 648 | 9, 791 | 10, 070 | 13, 227 | |
| `xj | 0, 343 | 0, 557 | 1, 021 | 0, 810 | 1, 178 | 1, 134 | 1, 093 | 1, 224 | 1, 119 | 1, 323 |
|
|

Если считать промоделированные значения xj интервалами времени между событиями, то можно изобразить схему простейшего потока событий.
T1 T2 T3
 |
1 2 3 4 5 6 7 8 9 10