
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Моделирование случайных величин, распределенных по различным законам
|
|
Биноминальный закон распределения позволяет определить вероятность появления различного числа событий при многократных испытаниях с неизменными условиями. Если известна вероятность появления события А при одном испытании P(А) = р и задано число испытаний n, то легко определить ряд распределения данной дискретной случайной величины, состоящий из n+1 членов.
| Х | … | k | … | n-1 | n | ||
| P | Pn(0) | Pn(1) | … | Pn(k) | … | Pn(n–1) | Pn(n) |
Вероятность появления k раз события A при n испытаниях (где k = 0, 1, 2, …, n) может быть определена по формуле Бернулли:
 , где
, где 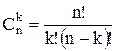 ; q = 1– p.
; q = 1– p.
На основе рассчитанного ряда можно построить график накопленных вероятностей и по нему с помощью случайных чисел статистически промоделировать случайную величину, распределенную по биноминальному закону.
Закон Пуассона так же, как и биноминальный, представляет собой распределение дискретной случайной величины. Для закона Пуассона Pt(m) является выражением, по которому вычисляется вероятность появления m раз (m = 1, 2, 3, ¼) события A за заданное время t:
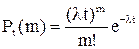 ,
,
где l - интенсивность потока событий, то есть число событий в единицу времени.
Чтобы промоделировать случайную величину, распределенную по закону Пуассона, используют тот же алгоритм моделирования.
Случайная величина, распределенная по закону равномерной плотности в заданном интервале от a до b, подчиняется следующим закономерностям:
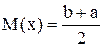 ,
, 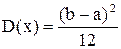 и
и
 ,
,  ,
, 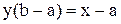 .
.
Разрешая последнее равенство относительно x, можно получить выражение для алгоритма моделирования данной случайной величины, распределенной по заданному равномерному закону,
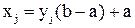 ,
,
где yj – равномерно распределенные случайные числа (0 £ yj £ 1).
Большое применение находят случайные величины, распределенные по нормальному закону или закону Гаусса. Интегральная функция нормального закона, как известно, не берется в конечном виде, то есть не выражается через элементарные функции. Поэтому моделирование случайной величины, распределенной по нормальному закону, может проводиться одним из следующих способов:
1) графическим;
2) обратным вычислением по таблице интегральной функции;
3) с помощью специальной таблицы случайных чисел, распределенных по квазинормальному закону;
4) с использованием случайных чисел, распределенных по закону равномерной плотности.
При графическом способе на основе функции плотности распределения строится график интегральной функции. Далее по таблице случайных чисел берутся числа 0 £ yj £ 1 и находятся соответствующие им реализации случайного числа хj (рис. 2).
Более точным и удобным является способ обратных вычислений по интегральной функции нормального распределения.
Плотность вероятности нормального закона выражается зависимостью
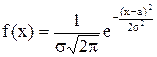 ,
,
где a – математическое ожидание случайной величины X (a = М(X));
s – среднее квадратическое отклонение.
Интегральная функция в этом случае
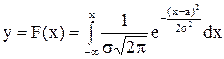 .
.
Приведенный интеграл не берется в конечном виде. Центрированием и нормированием он приводится к табличному виду. Для этого производится замена переменной интегрирования.
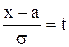 и dx = sdt
и dx = sdt
После подстановки получается
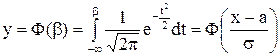 .
.
Выражение Ф(b) называется табличной интегральной функцией. Ее значения вычислены с помощью рядов и для нее составлены специальные таблицы.
Сущность обратных вычислений заключается в нахождении по таблице значения функции F и определении соответствующего ей аргумента. Исходя из сказанного
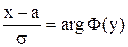 .
.
В таблице, как правило, даются значения функции от 0, 5, то есть одной половины, соответствующие положительным значениям аргумента. Отрицательные значения аргумента находятся, исходя из симметрии относительно оси ординат. В этом случае, разрешая приведенное равенство относительно x, можно получить выражение для алгоритма моделирования случайной величины, распределенной по нормальному закону, способом обратных вычислений
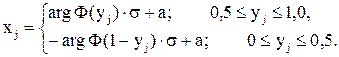
где yj – равномерно распределенные случайные числа (0 £ yj £ 1).
Случайная нормально распределенная величина также может быть промоделирована с помощью специальной заранее составленной таблицы. Числа в этой таблице являются псевдослучайными и соответствуют квазинормальному (ввиду приблизительности) нормированному и центрированному распределению, для которых a = 0 и s = 1. Использование этих чисел аналогично использованию таблицы случайных чисел.
Выражение для алгоритма моделирования случайных чисел, распределенных по нормальному закону, с использованием таблицы псевдослучайных чисел выглядит следующим образом:
 ,
,
где хj0 – псевдослучайные числа (-3 £ хj £ 3).
При использовании ЭВМ часто применяют способ генерирования нормально распределенной случайной величины, основанный на законе больших чисел, в частности на центральной предельной теореме Ляпунова. Согласно ей сумма нескольких независимых равномерно распределенных случайных величин, имеющих соизмеримые математические ожидания и дисперсии, соответствует асимптотически нормальному закону, для которого математическое ожидание суммы равно сумме математических ожиданий составляющих законов М(х) = М(х1)+М(х2)+¼ +М(хn) и дисперсия равна сумме дисперсий составляющих законов D(х) = D(х1)+D(х2)+¼ +D(хn).
Проверкой установлено, что достаточно сложить шесть чисел, подчиняющихся закону равномерной плотности, чтобы суммарный закон был нормальным. Для приведения его в соответствие по параметрам с моделируемым распределением необходимо произвести несложные операции по нормированию и центрированию суммарного распределения с последующим соответствующим его денормированием и децентрированием. Поэтому весьма удобно для моделирования случайных чисел, распределенных по нормальному закону, воспользоваться числами, распределенными по закону равномерной плотности.
Кроме рассмотренных выше точных способов моделирования случайных величин, распределенных по различным законам, существуют также приблизительные способы.
Пусть задана плотность вероятности какого-либо распределения, интеграл от которой не берется в конечном виде, то есть не выражается через элементарные функции. Указанная особенность имеет место для нормального закона, логарифмически нормального, гамма-распределения и при задании дифференциальной функции графиком. В этом случае можно поступить следующим образом:
1. Область возможных значений от a до b функции f(x) разбивается на n достаточно малых интервалов.
2. В каждом из интервалов любым известным способом находится площадь под кривой. Кривая на этом интервале заменяется отрезком прямой, исходя из условия равенства площадей под ними. Тем самым непрерывная функция заменяется дискретной кусочно-равномерной функцией.
3. Полученные площади масштабируются так, чтобы сумма всех площадей на интервале от a до b была равна 1.
4. Строится ряд накопленных вероятностей исследуемой случайной величины и далее она моделируется как обычная дискретная случайная величина.