
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Шар, цилиндр, конус и их изображение
|
|
Шар - одна из простейших фигур, обладающая разнообразными свойствами. Некоторые из них были известны еще древнегреческим математикам.
Поверхность шара называется сферой. Определяются сфера и шар аналогично тому, как определяются окружность и круг на плоскости.
Сферой называется множество точек пространства, удаленных от данной точки на заданное положительное расстояние. При этом данная точка называется центром сферы, а данное расстояние - ее радиусом.
Шаром называется множество точек пространства, находящихся от данной точки на расстоянии, не большем некоторого данного положительного расстояния. Данная точка - это центр шара, а данное расстояние - радиус шара.
 Заметим, что радиусом шара и сферы называют не только расстояние, но также любой отрезок, соединяющий их центр с точкой на сфере.
Заметим, что радиусом шара и сферы называют не только расстояние, но также любой отрезок, соединяющий их центр с точкой на сфере.
Диаметр шара и сферы - это любой отрезок, соединяющий две точки сферы и проходящий через центр, а также длина этого отрезка.
Если шар пересечь плоскостью, проходящей через его центр, то пересечением будет круг, радиус которого совпадает с радиусом шара. Этот круг называют большим кругом, а его окружность - большой окружностью или экватором.
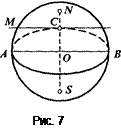
При параллельном проектировании шар изображается в виде круга того же радиуса. Чтобы сделать изображение шара более наглядным, рисуют проекцию какой-нибудь большой окружности, плоскость которой не перпендикулярна плоскости проекции. Эта проекция будет эллипсом. Центр шара изобразится центром этого эллипса (рис. 7). Теперь можно найти соответствующие полюсы N и S при условии, что отрезок, их соединяющий, перпендикулярен плоскости экватора. Для этого через точку О проводим прямую, перпендикулярную А В, и отмечаем точку С - пересечение этой прямой с эллипсом; затем через точку С проводим касательную к эллипсу, изображающему экватор. Доказано, что расстояние СМ равно расстоянию от центра шара до каждого из полюсов. Поэтому, отложив отрезки ОМ и 0S, равные СМ, получим полюсы N и S.
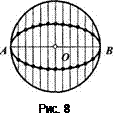 Рассмотрим один из приемов построения эллипса: строят окружность с диаметром и проводят хорды, перпендикулярные диаметру (рис. 8). Половину каждой из хорд делят пополам и полученные точки соединяют плавной кривой. Эта кривая - эллипс, большой осью которого является отрезок АВ, а центром - точка О.
Рассмотрим один из приемов построения эллипса: строят окружность с диаметром и проводят хорды, перпендикулярные диаметру (рис. 8). Половину каждой из хорд делят пополам и полученные точки соединяют плавной кривой. Эта кривая - эллипс, большой осью которого является отрезок АВ, а центром - точка О.
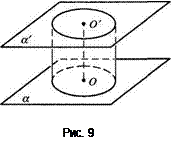 Этот прием можно использовать, изображая на плоскости круговой цилиндр и круговой конус. Мы будем рассматривать только прямой круговой цилиндр - геометрическое тело, образованное заключенными между двумя параллельными плоскостями отрезками всех параллельных прямых, пересекающих круг в одной из плоскостей, и перпендикулярных плоскостям оснований (рис. 9).
Этот прием можно использовать, изображая на плоскости круговой цилиндр и круговой конус. Мы будем рассматривать только прямой круговой цилиндр - геометрическое тело, образованное заключенными между двумя параллельными плоскостями отрезками всех параллельных прямых, пересекающих круг в одной из плоскостей, и перпендикулярных плоскостям оснований (рис. 9).
Радиусом цилиндра называется радиус окружности его основания. Высотой цилиндра называется расстояние между плоскостями его оснований. Его осью называется прямая, проходящая через центры окружностей оснований.
Конусом называется тело, образованное всеми отрезками, соединяющими данную точку - его вершину - с точками некоторого круга -основания конуса.
Отрезки, соединяющие вершину конуса с точками окружности основания, называются его образующими.
 Конус называется прямым, если прямая, соединяющая его вершину с центром окружности основания, перпендикулярна основанию.
Конус называется прямым, если прямая, соединяющая его вершину с центром окружности основания, перпендикулярна основанию.
Высотой конуса называется расстояние от его вершины до основания.
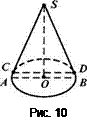
Прямой круговой конус изображают так. Сначала строят эллипс - основание, затем находят центр основания - точку О и перпендикулярно проводят отрезок OS, который изображает высоту конуса. Из точки S проводят к эллипсу касательные (это делают на глаз, прикладывая линейку) и выделяют отрезки SС и SD этих прямых от точки S до точек касания С и D. Заметим, что отрезок СD не совпадает с диаметром основания конуса (рис. 10).