
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
множество значений состоит шести чисел 1, 2, 3, 4, 5, 6,
|
|
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ (СВ).
1. основные понятия.
2. алфавит.
3. способы задания случайной величины.
3. 1. Закон распределения.
3. 2. Функция распределения.
3. 3. Плотность распределения (вероятности).
4. Основные характеристики СВ.
4. 1. Математическое ожидание.
4. 2. Дисперсия.
4. 3. Среднее квадратическое отклонение.
5. системы случайных величин.
1.
В примерах, с которыми мы встречались ранее, случайные события характеризовались с помощью чисел (число очков, выпавших при бросании игральной кости, число случаев брака при обследовании партии из n изделий и т. п.). В подавляющем большинстве усматриваемых в теории вероятностей задач исход опыта характеризуется некоторым числом. При этом случайный характер исхода влечет за собой случайность числа; это значит, что при повторении опыта число меняется непредвиденным образом.
Подбрасывается игральная кость; СВ - число выпавшихочков.
Покупается n лотерейных билетов; СВ — число выигрышей.
3. СВ - Число родившихся мальчиков среди ста новорожденных. 4.Электрическая лампа испытывается на длительность горения; СВ — полное время горения лампы.
Некто приходит на платформу станции метро, чтобы сесть в поезд; СВ — время ожидания ближайшего поезда.
СВ - Расстояние, которое пролетит снаряд при выстреле из орудия. Действительно, расстояние зависит не только от установки прицела, но и от многих других причин (силы и направления ветра, температуры и т. д.), которые не могут быть полностью учтены.
Чтобы все примеры подобного рода уложить в единую схему, введем понятие случайной величины.
Случайной величиной называется величина, которая в результате опыта принимает то или иное числовое значение, заранее неизвестно, какое - именно (это зависит от случая). Данное «определение» не претендует, конечно, на строгость; скорее его следует рассматривать как описаниепонятия случайной величины.
Каждой случайной величине X соответствует некоторое множество чисел. Это — множество значений, которые может принимать величина X.
множество значений состоит шести чисел 1, 2, 3, 4, 5, 6,
2. множество значений состоит из чисел 0, 1, 2, …, n,
3. случайная величина имеет следующие возможные значения: О, 1, 2,.... 100
4. X может принимать (в принципе) любое неотрицательное значение,
5. множество значений это отрезок [0, 2] числовой оси (поезда- метрополитена идут с интервалом в 2 минуты).
6.Возможные значения этой величины принадлежат некоторому промежутку (а, в).
Уже из сказанного можно заключить о целесообразности различать случайные величины, принимающие лишь отдельные, изолированные значения, и случайные величины, возможные значения которых сплошь заполняют некоторый промежуток.
Исходя из этого, различают в основном два вида случайных величин: дискретные (1 и 2 случаи), непрерывные (3 и 4 случаи).
Дискретныеслучайные величины характеризуются тем, что
могут принимать лишь конечное или счетное множество значений. Число возможных значений дискретной случайной величины может быть конечным или счетным.
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно.
2.
Для случайных величин действует алгебра событий. Только, будем обозначать случайные величины прописными буквами X, Y, Z… а их возможные значения — соответствующими строчными буквами х, у, z...
Например, если случайная величина X имеет три возможных значения, то они будут обозначены так: х1, х2, х3.
3.
На первый взгляд может показаться, что для задания случайной величины достаточно перечислить все ее возможные значения. Хотя различные случайные величины могут иметь одно и то же множество возможных значений.
Имеются две игральные кости, причем одна сделана из однородного материала, а другая, скажем, склеена из двух кусков разной плотности. Обозначим через X число очков выпадающих на первой кости, через У — число очков на второй. Случайные величины X и У имеют одно и то же множество значений (а именно {1, 2, 3, 4, 5, 6}), однако ведут себя совершенно по-разному. Если много раз подряд бросать первую из костей, то частоты событий X = 1, X = 2, …, X=6 будут близки к 1/6: при многократном же бросании второй кости частоты событий Y = 1, Y = 2,..., Y= 6 будут совсем другими.
Этот пример показывает, что знание одного лишь множества возможных значений недостаточно для полного описания случайной величины. Необходимо еще знать, какчасто случайная величина принимает то или другое из своих значений. Любое правило, устанавливающее связь между возможными значениями случайной величины и их вероятностями, называется законом распределенияслучайной величины.
3.2.
Функцией распределения случайной величины 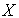 называется функция
называется функция  действительного переменного
действительного переменного  , определяющая вероятность того, что случайная величина
, определяющая вероятность того, что случайная величина 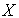 примет в результате реализации эксперимента значение, меньшее некоторого фиксированного числа
примет в результате реализации эксперимента значение, меньшее некоторого фиксированного числа  :
:  .
.
Если рассматривать случайную величину 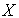 как случайную точку на оси
как случайную точку на оси  , то функция распределения
, то функция распределения  с геометрической точки зрения это вероятность того, что случайная точка
с геометрической точки зрения это вероятность того, что случайная точка 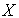 в результате реализации эксперимента попадет левее точки
в результате реализации эксперимента попадет левее точки  .
.
Функция распределения случайной величины 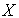 имеет следующие свойства:
имеет следующие свойства:
1) Очевидно, что функция  при любом
при любом  удовлетворяет неравенству
удовлетворяет неравенству  .
.
2) Функция распределения — неубывающая функция  , т.е. для любых
, т.е. для любых  и
и  , таких что
, таких что  , имеет место неравенство
, имеет место неравенство  .
.
Доказательство. Пусть  и
и 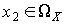 и
и  . Событие, состоящее в том, что
. Событие, состоящее в том, что 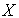 примет значение, меньшее, чем
примет значение, меньшее, чем  ,
,  представим в виде суммы двух несовместных событий:
представим в виде суммы двух несовместных событий: 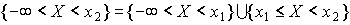 . Тогда согласно аксиоме 3 Колмогорова,
. Тогда согласно аксиоме 3 Колмогорова,  или по формуле
или по формуле  , откуда
, откуда  , так как
, так как  . Свойство доказано.
. Свойство доказано.
3) Теорема. Для любых  и
и  вероятность неравенства
вероятность неравенства 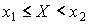 вычисляется по формуле
вычисляется по формуле 
Доказательство. Справедливость формулы следует из предыдущего свойства. Таким образом, вероятность попадания случайной величины 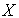 в полуинтервал
в полуинтервал  равна разности значений функции распределения вычисленных на концах полуинтервала
равна разности значений функции распределения вычисленных на концах полуинтервала  и
и  .
.
4) F(-¥) = 0; F(+¥) = 1 или 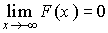 ;
; 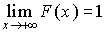 .
.
Доказательство. Пусть  и
и 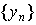 — две монотонные числовые последовательности, причем
— две монотонные числовые последовательности, причем 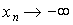 ,
, 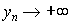 при
при  . Достоверное событие
. Достоверное событие  эквивалентно объединению событий
эквивалентно объединению событий 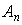 :
:  ;
;  .
.
Так как 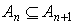 , то по свойству вероятностей
, то по свойству вероятностей  , т.е.
, т.е.  .
.
Принимая во внимание определение предела, получаем  ;
; 
4. Закон распределения полностью характеризует случайную величину. Иногда о
случайной величине достаточно знать не весь закон распределения, а лишь некоторые числа, которые описывают случайную величину обобщенно. Такие числа называются числовыми характеристиками случайной величины. Важнейшей числовой характеристикой случайной величины является математическое ожидание.
4.1.
Свойства математического ожидания:
1) математическое ожидание постоянной равно этой постоянной
M(C)=C (2.6)
2) постоянный множитель можно выносить за знак математического ожидания
М(СХ) = С • М(Х) (2.7)
3) математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых
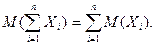
4) математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий сомножителей
М(Х1 • Х2 • … • Хn) = М(X1) • М(Х2) • … • М(Хn).
4.2.
Легко привести примеры случайных величин, имеющих одинаковые математические ожидания, но разные законы распределения.
На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее среднего. Оценка М (Х – M(X)) не подходит, так как М(Х–M(X))=M(X)–M(X)=О для любой случайной величины X.
Удобнее всего оценивать рассеяние вокруг математического ожидания, вычисляя среднее значения квадрата отклонения, которое называют дисперсией. D(X)=М(X–M(X))2=М(X2)–(M(X))2.
Свойства дисперсии:
1) дисперсия постоянной равна 0
D(C) = 0, (2.12)
2) дисперсия случайной величины, умноженной на постоянную, равна произведению квадрата постоянной на дисперсию этой случайной величины
D(CX) = С2 • DX; (2.13)
3) дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых
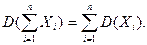
4) дисперсия суммы постоянной величины и случайной величины равна дисперсии случайной величины D(C + X) = DX;
5) дисперсия разности двух независимых случайных величин равна сумме их дисперсий D(X1 – Х2) = DX1 + DX2.
4.3.
 - называется среднем квадратическим отклонением.
- называется среднем квадратическим отклонением.
5.
Пусть имеется пространство элементарных событий U, на нем построено поле событий и для каждого события А из этого поля определена вероятность Р(А). Каждому элементарному событию gi из U сопоставим несколько чисел: Х i1, Х i2, Х i3,... Х in или вектор Хi. Потребуем, чтобы для любых хj (-∞ < хj < +∞), j = 1, 2... n, множество А тех g, для которых Х j < хj (j = 1, 2,... n), принадлежало полю событий, т.е. для него определена вероятность Р{ Х 1 < x1, Х 2 < x2,... Х n < xn } = P(A) = F(x1, x2,... xn). Тогда Х называется многомерной случайной величиной, или случайным вектором, а F(x1, x2,... xn) ее функцией распределения.
1. Координаты молекулы, находящейся в сосуде с газом, (x, y, z) или компоненты ее скорости (Vx, Vy, Vz) - можно рассматривать как трехмерные случайные величины
2. В задаче " о встрече" время прихода одного участника (х1) и другого (х2), если условия их прихода известны (скажем - любой момент в течение заданного часа), пару чисел х1, х2 можно рассматривать как двумерную случайную величину
3. Результат эксперимента, состоящего в измерении тока через разрядную трубку при десяти различных напряжениях, поданных на трубку, можно рассматривать как десятимерную случайную величину
Случайные величины могут быть зависимыми и независимыми. Случайные величины x и h называются независимыми, если для любых x 1, x 2  R 2 справедливо равенство: Fx , h (x 1, x 2)= Fx (x 1) Fh (x 2).
R 2 справедливо равенство: Fx , h (x 1, x 2)= Fx (x 1) Fh (x 2).
Если две случайные величины x и h зависимы, то информация о том, какое значение на самом деле приняла одна из них, меняет наше представление о распределении другой. В связи с этим можно ввести понятие условного распределения.
Многомерные случайные величины могут быть непрерывными, т.е. принимать любые значения в некоторой области n-мерного пространства (например, упомянутые выше компоненты скорости молекулы). Многомерные случайные величины могут быть дискретными, т.е. каждая компонента случайного вектора может принимать только конечное или счетное множество определенных значений.
Свойства многомерной функции распределения:
1. F(-∞... x1, x2,... xn) = 0
2. F(x1, x2,... xn-1, ∞) = F(x1, x2,... xn-1), т.е. если один из аргументов принимает значение ∞, то размерность случайной величины уменьшается на 1.
3. F(x1, x2,... xn) не убывающая функция любого аргумента
У них F(x1, x2,... xn) непрерывная функция всех аргументов. Для них определена n-мерная плотность распределения p(x1, x2,... xn), которая есть производная от функции распределения.
Свойства плотности распределения:
1. Вероятность того, что случайный вектор примет значение, лежащее в области V n-мерного пространства, равна интегралу по этой области от n-мерной плотности распределения.
2. Интеграл по всем переменным от - ∞ до + ∞ от n-мерной плотности распределения равен 1.
3. Интеграл по одной переменной от - ∞ до + ∞ от n-мерной плотности распределения равен плотности распределения (n-1)-мерной случайной величины.
|