
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры случайных величин
|
|
РАЗДЕЛ I. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Понятие случайной величины
Определение 1. Случайной величиной называется такая переменная величина, которая в результате испытания со случайным исходом принимает то или иное значение из множества всех возможных значений.
Случайные величины обозначаются заглавными буквами конца латинского алфавита X, У, Z, а их значения обозначаются соответственно малыми буквами х, у, z.
Случайные величины бывают двух основных видов: дискретные и непрерывные.
Определение 2. Дискретной случайной величиной называется такая случайная величина, значения которой конечно или счетно, т.е. её значения можно пронумеровать. В противном случае случайная величина называется непрерывной.
Значения дискретной случайной величины изолированы друг от друга, значения непрерывной случайной величины сплошь занимают некоторый промежуток.
Примеры случайных величин
№1. Испытание - бросание игральной кости. Случайные исходы испытания - число выпавших очков (1, 2, 3, 4, 5, 6). В этом случае случайной величиной X является число выпавших очков. Множество всех значений можно перенумеровать:
х1 = 1; х2 = 2; х3 = 3; х4 = 4; х5 = 5; х6 = 6.
х - дискретная случайная величина.
№2. Испытание - ведется отбор изделий из множества изделий различного качества до первого появления изделия высокого качества. В этом случае случайной величиной У является число проб, которое нужно произвести до появления изделия высокого качества. Множество всех возможных значений бесконечно,
у1 =1; у2 = 2; у3=3; …; уn=n…
у - дискретная случайная величина.
№3. Испытание - время работы двигателя. Случайной величиной Т является время работы двигателя до первого отказа. Множеством значений Т являются различные промежутки: [0; t1]; [0; t2];...; [0; t3];...
Случайная величина Т - непрерывная, её значения  .
.
№4. Испытание - измерение длины ступни наугад взятого человека. Случайной величиной является Z - длина ступни. Множество всех возможных значений теоретически 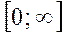 .
.
Z - непрерывная случайная величина. Для того, чтобы описать, задать случайную величину нужно знать не только множество значений, которое она принимает, но и вероятности с которыми принимаются те или иные значения или промежутки значений.
Соотношение, указывающее на то, как значения вероятности (0 ≤ Р ≤ 1) распределяются между значениями случайной величины называется законом распределения.
Законы распределения случайной величины могут быть различными, но записываются они, как правило, тремя способами аналитической записи.
Дискретная случайная величина, как правило, задается в виде ряда распределения. Непрерывная - в виде f(x) - функции плотности распределения и в виде функции распределения F(x) может задаваться как дискретная так и непрерывная случайная величина.
Определение 3. Ряд распределения дискретной случайной величины - это таблица устанавливающая связь между вероятностью и каждым, любым значением случайной величины.
| хi | x1 | x2 | … | xn | |
| pi | p1 | p2 | … | pn | |
где 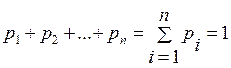
|
если множество значений дискретной случайной величины конечно.
или
| хi | x1 | x2 | … | xn | ... |
| pi | p1 | p2 | … | pn | … |
где 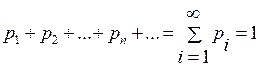
|
если множество значений дискретной случайной величины бесконечно.
Определение 4. Функция распределения F(x) - это функция, устанавливающая связь между вероятностью и промежутком значений случайной величины от 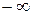 до х,
до х,  , где х - текущее, любое значение случайной величины.
, где х - текущее, любое значение случайной величины. 
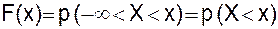
Функция F(x) характеризует вероятность того, что случайная величина X примет значение меньшее, чем некоторое значение х (т.е, попадет левее х).
Если случайная величина принимает любые значения от 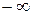 до
до 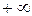 то тот факт, что вероятность (0 ≤ Р ≤ 1) распределяется между промежутками значений ]
то тот факт, что вероятность (0 ≤ Р ≤ 1) распределяется между промежутками значений ] 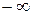 ; х [, означает, что F(
; х [, означает, что F(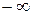 ) = 0; F(
) = 0; F(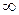 ) = 1. Если значения случайной величины сосредоточены в некотором промежутке [ a; b ], то тот факт, что вероятность распределяется между промежутками вида ]
) = 1. Если значения случайной величины сосредоточены в некотором промежутке [ a; b ], то тот факт, что вероятность распределяется между промежутками вида ] 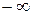 ; х[, где х
; х[, где х 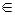 [ а; b ] означает, что
[ а; b ] означает, что
F (a) =P(X< a) =0 и F (b) =P(X< b) =1
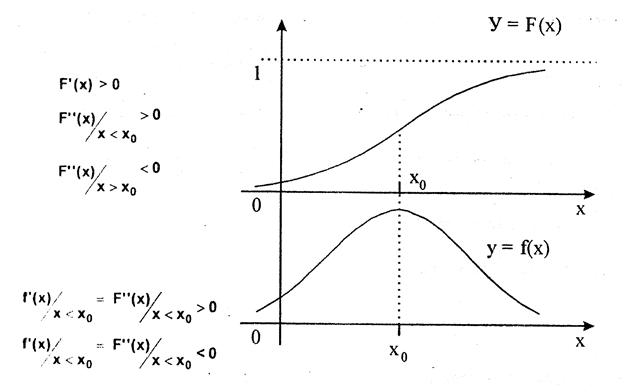
Отметим, что, если X - дискретная случайная величина, то график у = F(x) -дискретная прерывная линия, если X - непрерывная, то и график у = F(x) изображается в виде непрерывной линии.
Пример №1. Пусть Х - дискретная случайная величина, заданная рядом распределения:
| хi | ||||||
| pi | 0, 2 | 0, 1 | 0, 2 | 0, 3 | 0, 1 | 0, 1 |
Задать данную случайную величину с помощью функции распределения, вычислить вероятность попадания случайной величины научасток [1, 7].
| F{x) |
 Решение. По определению F(x) = Р (X < х), где х < 0; 0 ≤ х < 1; 3≤ х< 5; 5≤ х< 7; 7≤ х< 9; 9≥ х. Тогда
Решение. По определению F(x) = Р (X < х), где х < 0; 0 ≤ х < 1; 3≤ х< 5; 5≤ х< 7; 7≤ х< 9; 9≥ х. Тогда
0; если х< 0
0, 2; если 0≤ х< 1
|
0, 2+0, 1+0, 2=0, 5 если 3≤ х< 5
0, 2+0, 1+0, 2+0, 3=0, 8 если 5≤ х< 7
0, 2+0, 1+0, 2+0, 3+0, 1=0, 9 если 7≤ х< 9
0, 2+0, 1+0, 2+0, 3+0, 1+0, 1=1 если х≥ 9
Отметим, что F(a)= F(0)=0; F(b)= F(9)= 1
График y =F(x) имеет вид:
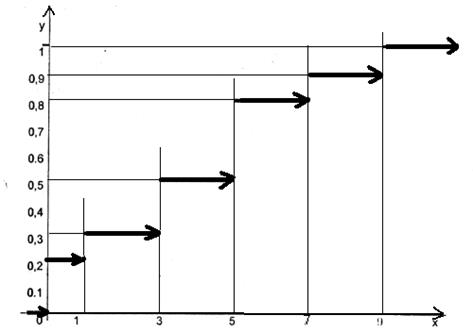
Найдем P(1< x< 7)
Известно, что P(α < x< β)=F(β)-F(α),
Тогда P(1< x7)=F(7)-F(1)=0, 8-0, 2=0, 6
Определение №5.
Функция плотности распределения у=f(x) - это функция, устанавливающая связь между вероятностью, приходящейся на как угодно малый промежуток значений случайной величины, к величине этого промежутка:
| cht |
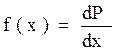 ,
,
где dP - элемент вероятности (0 ≤ Р ≤ 1),
dx - величина промежутка.
Так как F(x) = Р (Х < х), то f(x) = F' (х)
Действительно: dP(X < х) = dF(x) = F'(x)dx,
но 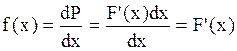
На основании того, что f(x)=F’(x), зная график функции y=F(x) можно графически изобразить и функцию y=f(x).
Если известна функция плотности распределения у=f(х), то функция распределения у=F(x) находится по формуле  . Действительно:
. Действительно:

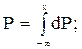 и
и 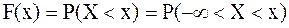
тогда 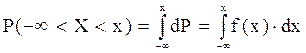 итак,
итак, 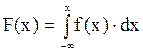
Замечание. Функцию F(x) часто называют интегральной функцией распределения, a f(x) - дифференциальной.
Вероятность того, что непрерывная случайная величина X примет промежуток значений от α до β (попадает в интервал [ α; β ] находится по формуле
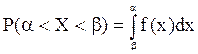
Если значения случайной величины сосредоточены в промежутке [ a; b],
то 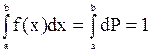
Если на всей числовой оси, то 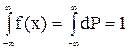
Пример №2. Найти у = f(x) и Р(0 < х < 5),
|
 0; при х< 0
0; при х< 0
Aх2; при 0≤ x< 7
1; при х≥ 7
Построить графики у = f(x) и у = F(x)
Решение 1. Найдем неизвестный коэффициент А из условия F(b) = 1, если x Є [а; b]. В данном случае [a; b] это [0; 7], следовательно F(7)=1, т.е.
А(7)2 =1; А49=1; А=1/49. 
0; при х< 0
|
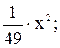 при 0 ≤ х < 7
при 0 ≤ х < 7
1; при х ≥ 7
 2. Известно, что f(x)= F/(x). Если х< 0, то F(x)= 0 f(x)=F/(x)=(0)/=0.
2. Известно, что f(x)= F/(x). Если х< 0, то F(x)= 0 f(x)=F/(x)=(0)/=0.
Если 0≤ х< 7, то 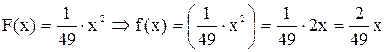
Если х≥ 7, то 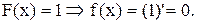
 0; при х < 0
0; при х < 0
|
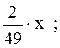 при 0 ≤ х < 7
при 0 ≤ х < 7
1; при х ≥ 7
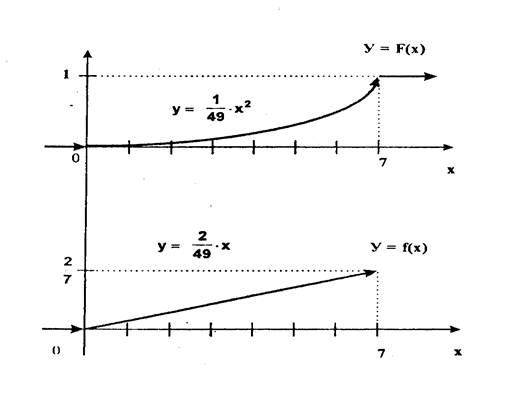 Найдем P(1< x< 7)=F(7)-F(x)=0, 8-0, 2=0, 6
Найдем P(1< x< 7)=F(7)-F(x)=0, 8-0, 2=0, 6
Найдем Р(0 < х < 5).
Известно, что 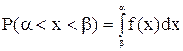 или Р (α < х < β) = F(b)-F(a)
или Р (α < х < β) = F(b)-F(a)
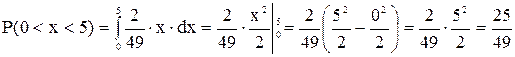 или
или
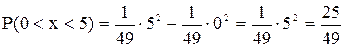
| 2 5 |
Пример №3.
Найти у = F(x), P(0 < х < 5)
 0; при х< 0
0; при х< 0
|
0; при х≥ 7
Решение. Найдем А из условия 
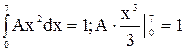
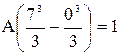
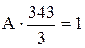
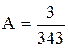
 0; при х< 0
0; при х< 0
|
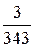 х2; при 0≤ x< 7
х2; при 0≤ x< 7
1; при х≥ 7
Найдем F(x) из условия 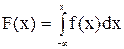
Если x< 0, то 
Если 0≤ х< 7, то 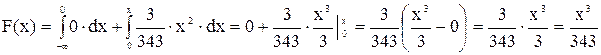
Если х≥ 7, то 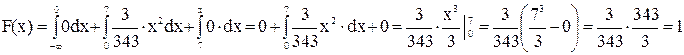
 0; при х< 0
0; при х< 0
|
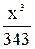 ; при 0≤ x< 7
; при 0≤ x< 7
1; при х≥ 7
Найдем P(0< x< 5)=F(5)-F(0)
P(0< x< 5)= 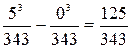
Замечание: Для закрепления данных понятий рекомендуется самостоятельно выполнить аналогичные задания из раздела
«ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ»