
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Математическое ожидание и дисперсия
|
|
Определение 1. Математическое ожидание - это число, характеризующее центр распределения.
Для дискретной случайной величины математическое ожидание вычисляется как сумма произведений значений случайной величины на соответствующие вероятности, т.е.
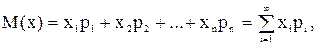 если число значений случайной величины конечно.
если число значений случайной величины конечно.
 если число значений случайной величины бесконечно, то М(х) существует, если сходится данный ряд.
если число значений случайной величины бесконечно, то М(х) существует, если сходится данный ряд.
Для непрерывной случайной величины математическое ожидание вычисляется через определенный интеграл от случайной величины х, умноженной на элемент вероятности dP = f(x)dx, т.е.
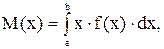
если значения случайной величины сосредоточены в [а; b].
и 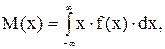
если значения случайной величины занимают всю числовую ось. В этом случае M(x) существует, если сходится несобственный интеграл.
Математическое ожидание называют также средним значением случайной величины. Оно имеет те же самые единицы измерения, что и случайная величина.
Определение 2. Дисперсия - это число, характеризующее отклонение случайной величины от центра распределения в квадратных единицах измерения случайной величины.
Дисперсия для любой случайной величины определяется как математическое ожидание квадрата отклонения случайной величины от математического ожидания, т.е.
D(x) = М (х – М (х))2
Эта формула имеет вид:
 т.к.
т.к.  если случайная величина дискретная.
если случайная величина дискретная.
Если случайная величина непрерывная, то
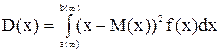 т.к.
т.к. 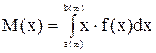
.Дисперсию можно также вычислить как разность математического ожидания квадрата случайной величины и квадрата математического ожидания случайной величины, т.е. по следующей формуле:
D(x) = М (х2) – М2 (х),
где  , если случайная величина дискретная.
, если случайная величина дискретная.
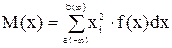 если непрерывная.
если непрерывная.
Определение 3. Средним квадратическим отклонением называется число равное арифметическому значению корня квадратного из дисперсии.
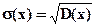
Среднее квадратическое отклонение имеет те же самые единицы измерения, что и случайная величина.
Пример №1. Найти М(х), D(x), σ (x), дискретной случайной величины, если
| хi | |||||
| pi | 0.3 | 0.1 | 0.3 | 0.2 | 0.1 |
Решение. Найдем математическое ожидание: 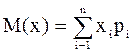

Найдем дисперсию: 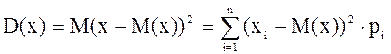
D(x)=(0-2, 7)20, 3+(1-2, 7)20, 1+(3-2, 7)20, 3+(5-2, 7)20, 2+(7-2, 7)20, 1=5, 41
или D(x)=M(x2)-M2(x);
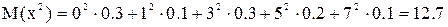
D(x) = 12, 7-(2, 7)2 = 5, 41
Найдем среднее квадратическое отклонение: 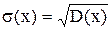
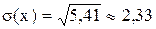
Пример №2. Найти M(х), D(x), σ (x) непрерывной случайной величины, если
 0; если х< 0
0; если х< 0
|
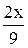 ; если 0≤ x< 3
; если 0≤ x< 3
0; если х≥ 3
Решение. Найдем математическое ожидание: 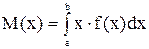
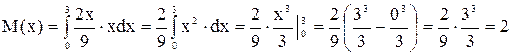
Найдем дисперсию по формуле:

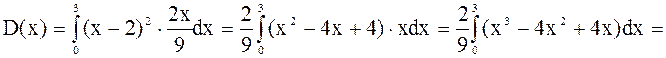

Найдем дисперсию по формуле: D(x) = М(х2) - М2(х)



D(x)= 4, 5-(2)2 =4, 5-4 = 0, 5
Найдем среднее квадратическое отклонение: 
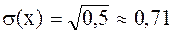
Замечание. Числовые характеристики M(x) и D(x) имеют следующие свойства:
 |
1. М(с) = с
2 М(к х) = кМ(х)
3 М(х ± у) = М(х) ± М(у)
4. М(х ± с) = М(х) ± с
5 М(ху) = М(х)М(у), если х и у - независимые случайные величины
1. D(c) = 0
2. D(kx) = k2D(x)
3. D(x ± у) = D(x) ± D(y), если х и у - независимые случайные величины.
4. D(x ± с) = D(x)