
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные законы распределения
|
|
1.Биномиальное распределение. Говорят, что случайная величина х подчиняется биномиальному закону распределения, если её возможные значения: О, 1, 2,..., т,..., п принимаются ею с вероятностями, вычисляемыми по формуле Бернулли:
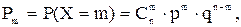
где 0< p< 1, q=1-p, 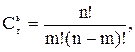 m=0, 1, 2, …, n
m=0, 1, 2, …, n
Биномиальное распределение имеет два параметра " n " и " р " (n -число всех возможных значений случайной величины или число независимых испытаний;
р - вероятность появления некоторого события А е единичном испытании).
Числовые характеристики случайной величины, подчиняющейся биномиальному закону распределения следующие;
М(х) = М(n) = np
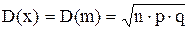
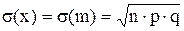
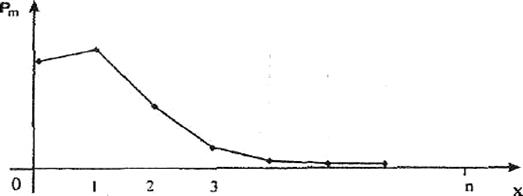
2. Распределение Пуассона.
Говорят, что случайная величина подчиняется распределению Пуассона, если её возможные значения: 0, 1, 2,..., m, …, n,... принимаются с вероятностями, вычисляемыми по формуле Пуассона:

Где m=0, 1, 2, …;
Распределение Пуассона имеет один параметр λ. Параметр в зависимости от условий задач может вычисляться по различным формулам:
λ = np; n - число независимых испытаний, р - вероятность появления события А в единичном испытании;
λ = λ ОТ, где λ 0 - некоторое среднее число событий, наступающих в единицу времени; Т - весь промежуток времени; или
λ = λ ОS, где λ 0 - некоторое среднее число событий, приходящихся на область, площадью в одну квадратную единицу, S - площадь всей области, и т.д.
Полигон распределения Пуассона:
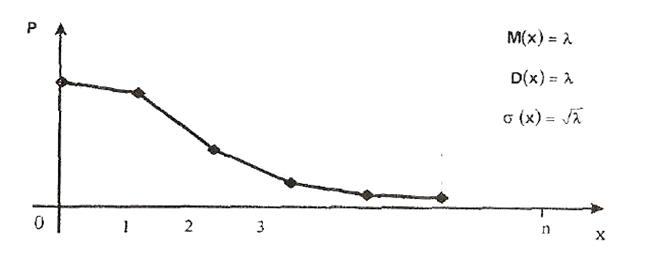
3. Геометрическое распределение. Говорят, что случайная величина X подчиняется геометрическому закону распределения, если её возможные значения: 0, 1, 2,..., m,..., n,... принимаются с вероятностью Р = qm p, где 0 < р < 1; q = 1-p; m = 0, 1, 2,...
Полигон распределения:
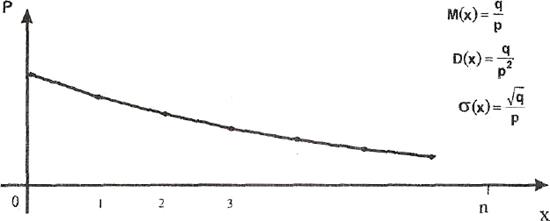
Геометрическое распределение имеет место в случае, когда производятся независимые испытания до первого появления некоторого события, которое в единичном испытании появляется с вероятностью р, а не появляется с вероятностью q.
На практике чаще всего встречается распределение геометрическое, сдвинутое на единицу, так как счет начинается не с нуля, а с единицы.

4. Гипергеометрическое распределение. Говорят, что случайная величина X подчиняется гипергеометрическому распределению с параметрами а, b, n, если её возможные значения; 0, 1, 2,..., m,..., nпринимаются с вероятностью:
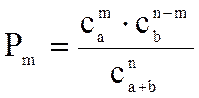
где m =0, 1, 2, …, n..

|
Полигон распределения:
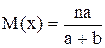
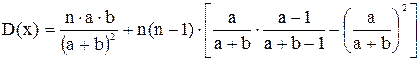
Гипергеометрическое распределение возникает при условиях, когда имеется урна, в которой " b " - белых и " а " - черных шаров; из урны извлекается " n " - шаров, тогда число белых шаров среди вынутых - это Х - случайная величина.
5. Показательное распределение. Говорят, что случайная величина X подчиняется показательному закону распределения, если
|
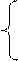 0; если х≤ 0
0; если х≤ 0
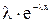 ; если х> 0
; если х> 0

|
где λ - параметр
6. Равномерное распределение. Говорят, что случайная величина подчиняется закону равномерной плотности распределения, если
|
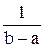 ; если
; если 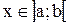
0; если 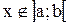
где a и b –параметры

7. Нормальное распределение. Говорят, что случайная величина X подчиняется нормальному закону распределения (закону Гаусса), если

где a, σ – параметры.

|
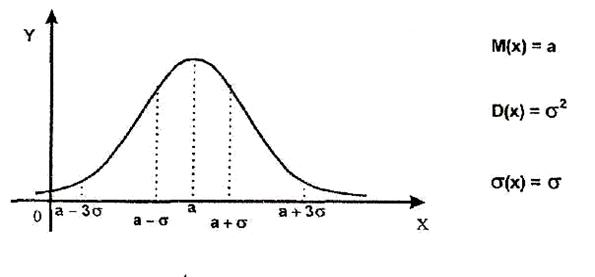
Основные формулы вычисления вероятностей в случае нормально и приближенно нормального распределения случайной величины:

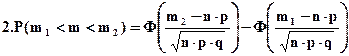
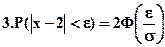
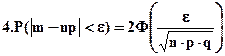

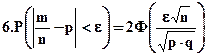 , где
, где 