Функция распределения

Функцией распределения случайной величины X называется функция F_X(x), определенная для любого действительного х и выражающая вероятность того, что случайная величина X примет значение, меньшее х:

F_X(x)=P(X< x).

Функция распределения обладает следующими свойствами:

1. Для любого 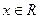справедливо неравенство 0£ F_X(x)£ 1.

2. Функция распределения является неубывающей функцией, то есть, если F_X(x₁) ≤ F_X(x₂), если х₂< х_1.

3. Вероятность того, что случайная величина примет значение из полуинтервала [x₁, x₂), равна разности значений функции распределения на концах интервала, то есть P(x₁£ X< x₂)=F_X(x₂)-F_X(x₁).

4. Если возможные значения случайной величины расположены на всей числовой прямой, то справедливы следующие предельные соотношения

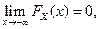
5. Функция распределения непрерывна слева, то есть F_X(x)=F(a).

6. Справедливо равенство: P(X³ x)=1-F_X(x).

Задача 2. Построить функцию распределения F_X(x) для случайной величины X из задачи 1.

Решение. Случайная величина X имеет три значения 1, 2, 3, которые делят всю числовую ось на четыре интервала: 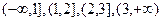. Если x≤ 1, то неравенство X< x невозможно (левее x нет значений случайной величины X) и значит, для такого x функция F_X(x)=0.

Если 1< x≤ 2, то неравенство X< x возможно только если X=1, а вероятность такого события равна 1/3, поэтому для таких x функция распределения F_X(x)=1/3.

Если 2< x≤ 3, неравенство X< x означает, что или X=1, или X=2, поэтому в этом случае вероятность P(X< x)=P(X=1)+P(X=2)=2/3, т.е. F_X(x)=2/3.

И, наконец, в случае x> 3 неравенство X< x выполняется для всех значений случайной величины X, поэтому P(X< x)=P(X=1)+P(X=2)+P(X=3)==1, т.е. F_X(x)=1.

Итак, мы получили следующую функцию: