
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дискретный случайный вектор.
|
|
Пусть на одном и том же пространстве элементарных исходов W заданы две случайные величины X и Y, принимающие значения хi (i = 1, 2,...) и уj (j = 1, 2,...), соответственно. Упорядоченная пара (X, Y) называется случайным вектором или двумерной случайной величиной. Совместный закон распределения вероятностей дискретных величин X и Y задается вероятностями 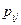 одновременного осуществления событий {X = хi} и {Y = уj}:
одновременного осуществления событий {X = хi} и {Y = уj}: 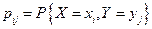
и представляется в виде таблицы
| X \ Y | y1 | y2 | … | ym |
| x1 | 
| 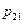
| … | 
|
| x2 | 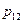
| 
| … | 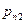
|
| … | … | … | … | … |
| xn | 
| 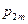
| … | 
|
При этом 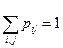 .
.
Вероятность события типа {(X, Y)Î В} — «случайная точка (X, Y) попадает в заданную область В» — вычисляется по формуле
 ,
,
т.е. суммирование идет по всем возможным парам (хi, yj) значений случайных величин X, h, для которых соответствующая точка (xi yj) входит в область В.
Частным законом распределения случайной величины X называется вероятность события {X = хi}. Если задан совместный закон распределения, то частный закон распределения для X можно получить с помощью формулы:
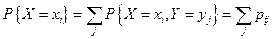 .
.
Аналогично, частным законом распределения h называется вероятность события {Y = yi}, которую также можно вычислить с помощью формулы:
 .
.
Дискретные случайные величины X, Y называются независимыми, если их совместный закон распределения представляется в виде произведения их частных законов распределения:
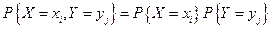 для всех значений хi и уj,
для всех значений хi и уj,
то есть если независимы случайные события {X = хi} и {Y = уj}.
Задача 3. Совместный закон распределения случайных величин X и Y задан c помощью таблицы
| X \ Y | ||
| -1 | 1/16 | 3/16 |
| 1/16 | 3/16 | |
| 1/8 | 3/8 |
Вычислить частные законы распределения составляющих величин X и Y, определить, зависимы ли они?
Решение. Частное распределение для X получается суммированием вероятностей в строках:
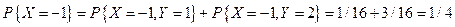 ;
;
 ;
;
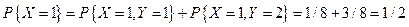 .
.
Аналогично получается частное распределение для Y:
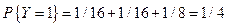 ;
;
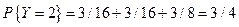 .
.
Полученные распределения можно записать в ту же таблицу напротив соответствующих значений случайных величин:
| X \ Y | |||
| -1 | 1/16 | 3/16 | ¼ |
| 1/16 | 3/16 | ¼ | |
| 1/8 | 3/8 | ½ | |
| 1/4 | 3/4 |
Теперь ответим на вопрос о независимости случайных величин X и Y. Для этого в каждой клетке совместного распределения вычислим произведение  и сравним его со значением вероятности
и сравним его со значением вероятности 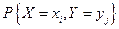 в этой клетке. Например, в клетке для значений X =-1 и Y=1 стоит вероятность 1/16, а произведение соответствующих частных вероятностей 1/4× 1/4 равно 1/16, т.е. совпадает с совместной вероятностью. Это условие проверяется во всех оставшихся пяти клетках, и оно оказывается верным во всех этих клетках. Следовательно, случайные величин X и Y независимы.
в этой клетке. Например, в клетке для значений X =-1 и Y=1 стоит вероятность 1/16, а произведение соответствующих частных вероятностей 1/4× 1/4 равно 1/16, т.е. совпадает с совместной вероятностью. Это условие проверяется во всех оставшихся пяти клетках, и оно оказывается верным во всех этих клетках. Следовательно, случайные величин X и Y независимы.