Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Степенные средние.
|
|
ТЕМА 5. Статистические показатели: средние ВЕЛИЧИНЫ
Степенные средние.
Средние величины играют исключительно большую роль в статистике. Средние величины представляют собой наиболее распространенную форму сводных величин. Они дают общую количественную характеристику элементов массового процесса. Средние величины являются как бы «представителями» всего ряда наблюдений, поскольку вокруг них концентрируются наблюдаемые значения признака. В сущности, средняя величина характеризует однородную совокупность одним числом. Например: средняя температура воздуха в аудитории.
Средняя обладает тем хорошим свойством, что в ней погашаются отклонения отдельных величин от основного типа.
Средняя величина – обобщающая характеристика изучаемого признака в исследуемой совокупности. Она отражает его типичный уровень в расчете на единицу совокупности в конкретных условиях места и времени.
Условиями применения средних величин являются: наличие качественно однородной совокупности и достаточно большой ее объем.
Пример. Рабочие бригады имеют следующую месячную заработную плату (табл. 5.1):
Таблица 5.1
Заработная плата рабочих
| Рабочий | Всего: | ||||||||||
| Зарплата, грн. | Всего: |
Требуется определить среднюю месячную зарплату рабочих бригады:
Средняя зарплата рабочего составляет 855 грн.
Существуют две категории средних величин: степенные средние (к ним относятся средняя арифметическая, средняя геометрическая и др.), а также структурные средние (мода и медиана). Выбор того или иного вида средней производится в зависимости от цели исследований, экономической сущности усредняемого показателя и характера имеющихся исходных данных.
Общая формула степенной средней имеет вид:
(5.1)
где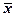 
– средняя статистического признака, а черта – знак символизирующий
процесс осреденения индивидуальных значений;
х – величина, для которой вычисляется средняя – осредняемый признак;
m – показатель степени средней;
n - количество наблюдений (объем совокупности).
Подставляя различные значения т, получают различные формы средних величин.
Средняя арифметическая (при т = 1) используется для осреднения прямых значений признаков путем их суммирования. Ее логическая формула имеет вид:
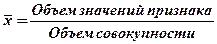(5.2)
Если данные не сгруппированы, применяется средняя арифметическая простая:
, (5.3)
где х – отдельные значения признака;
п – объем совокупности.
По формуле средней арифметической простой вычисляются также средние в хронологическом ряду, если интервалы времени, за которое приводятся значения признаков, равны.
Если в хронологическом ряду приведены моментные показатели, то для вычисления cредней они заменяются полусуммами значений на начало и конец периода. Если моментов более двух и интервалы между ними равны, то средняя вычисляется по формуле средней хронологической простой.
, (5.4)
где п – число моментов времени.
Если данные сгруппированы, то используют среднюю арифметическую взвешенную:
или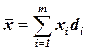 
, (5.5)
где fi – частота, di – частость i -й группы.
При этом 
а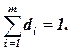 
Осреднению подлежат не только отдельные значения вариант, но и их групповые средние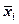 
, тогда весом будет частота (частость) каждой группы:
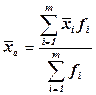(5.6)
Вычисленная таким способом средняя из групповых средних называется общей.
Весом может быть также абсолютная величина, логически связанная с осредняемым показателем. Выбор весов основывается на логической формуле показателя. Поскольку средняя величина вычисляется из расчета на единицу совокупности, то вес всегда будет находиться в знаменателе логической формулы. Например, при определении средней суммы затрат на одно рекламное объявление весом будет количество рекламных объявлений. При вычислении средней суммы затрат на одного рекламодателя весом будет количество рекламодателей.
Средняя арифметическая имеет определенные математические свойства, раскрывающие ее сущность. Так, сумма отклонений отдельных вариант от средней равна нулю, а сумма квадратов таких отклонений приближается к минимуму. Эти два свойства лежат в основе изучения вариации признаков.
Если отдельные значения вариант увеличить (уменьшить) на одну и ту же величину А или в k раз, то средняя изменится соответственно.
Например, если денежные вклады граждан в сбербанк скорректировать на уровень инфляции, составляющий 1, 2, то средний размер вклада увеличится соответственно в 1, 2 раза.
Средняя не изменится при пропорциональном изменении всех весов, но ее размер изменится, если произойдут структурные сдвиги.
Например, при неизменной курсовой стоимости акций отдельных эмитентов средняя стоимость акций может увеличиться за счет увеличения доли " дорогих" акций в общем количестве их продажи.
Указанные свойства средней используют в случае осреднения признаков порядковой (ранговой) шкалы. Для 3-х бальной шкалы варианты признака можно оцифровать порядковыми рангами R = 1, 2, 3или центрированными R 0 = - 1, 0, 1.
Средний центрированный балл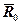 
отклоняется от среднего порядкового 
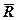на величину 
:
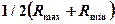(5.7)
Аналитические возможности среднего центрированного балла шире, чем среднего порядкового, т.к. 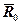может принимать положительные или отрицательные значения и свидетельствует о положительной или отрицательной оценке явления. Кроме того, поскольку средний центрированный балл не зависит от размерности шкалы, его используют для сравнения оценок разных явлений.
Пример. В таблице 5.2 приведены данные об отношении населения к приватизации земли. Определим уровень поддержки приватизации земли населением.
Табл. 5.2
Отношение населения к приватизации земли
| Отношение к приватизации | Доля ответов, % | Ранги | |
| Rj | R0 | ||
| Полностью поддерживаю | |||
| Частично поддерживаю | |||
| Не поддерживаю | -1 | ||
| Итого | – | – |
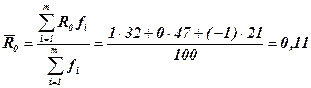
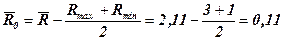
Следовательно, уровень поддержки приватизации земли положительный, но пока невысокий.
Средняя гармоническая (т = – 1) используется для осреднения индивидуальных значений признаков из обратных величин путем их суммирования. Для несгруппированных данных используется средняя гармоническая простая
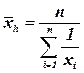(5.8)
Если данные сгруппированы, то используют среднюю гармоническую взвешенную
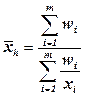, (5.9)
где wi – объем значений признака, т.е.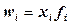 
Пример. Определить среднюю цену единицы продукции, если известны
(табл. 5.3) следующие данные:
Таблица 5.3
Данные о стоимости продукции
| Продукция | Цена, грн., хi | Сумма реализации, тыс., грн., wi | Частота случаев, fi = wi / xi |
| А | |||
| Б | |||
| В | |||
| ИТОГО: |
Средняя цена единицы продукции равна сумме реализации деленной на количество реализованных единиц. Сумма реализации (числитель) – известна, а количество реализованной продукции (знаменатель) – неизвестна. В таком случае, среднюю цену единицы продукции определяют по формуле средней гармонической:
.
Если бы для расчета мы использовали среднюю арифметическую простую, то получили бы неверный результат:
.
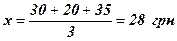Очевидно, что среднюю гармоническую взвешенную целесообразно использовать в тех случаях, когда отсутствует информация о значении знаменателя логической формулы, т.е. отсутствуют веса (когда статистическая информация не содержит конкретных частот по отдельным вариантам совокупности, а представлена только как их произведение).
Рассчитывать среднюю гармоническую взвешенную можно и в том случае, когда отдельные значения вариантов не указаны, а известны только итоги (суммарные значения числителя и знаменателя) логической формулы.
Средняя геометрическая (т = 0) определяется как произведение относительных величин динамики xij, рассчитанных как отношение i -го значения показателя к предыдущему (i – 1).
Формула средней геометрической простой
(5.10)
где 
- символ произведения;
– число осредняемых величин.
Средняя квадратическая (т = 2) используется для характеристики вариации и будет рассматриваться в следующей лекции (тема 6).
Вопрос о том, какой вид средней необходимо применить, решается в каждом конкретном случае путем анализа изучаемой совокупности, определяется материальным содержанием изучаемого явления, а также исходя из осмысления результатов исследований. В статистике правильную характеристику совокупности можно получить при использовании только определенного вида средней, установить которую помогает анализ. Для правильного выбора вида средней величины необходимо составить логическую схему.
Пример. Имеется цех, в котором работает 100 человек. Необходимо определить среднюю зарплату одного рабочего. Среднюю зарплату определим по логической формуле:
