
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ВСЕ недостающие степени (и (или) свободные члены) без пропусков записываем в ОБОИХ многочленах с нулевыми коэффициентами.
|
|
Теперь маленькая задачка, на какой множитель нужно умножить 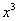 , чтобы получить
, чтобы получить 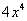 ? Очевидно, что на
? Очевидно, что на 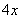 :
:

Далее умножаем 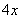 сначала на
сначала на 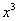 , потом – на
, потом – на 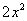 , потом – на
, потом – на  , потом – на 0 и записываем результаты слева:
, потом – на 0 и записываем результаты слева:
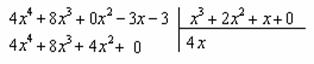
Проводим черточку и производим вычитание (из верха вычитаем низ):
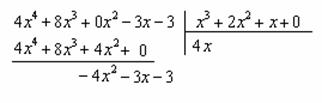
Старшая степень остатка  равна двум, старшая степень делителя
равна двум, старшая степень делителя  – больше, она равна трём, значит, больше разделить не удастся. Если бы изначально у нас был в числителе многочлен пятой степени, то то алгоритм деления увеличился бы на один шаг.
– больше, она равна трём, значит, больше разделить не удастся. Если бы изначально у нас был в числителе многочлен пятой степени, то то алгоритм деления увеличился бы на один шаг.
Итак, наше решение принимает следующий вид:
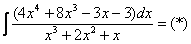
Делим числитель на знаменатель:
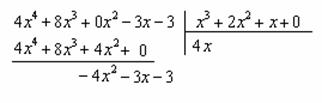

(1) Что дало деление? Много хорошего: теперь у нас два слагаемых, первое – интегрируется совсем просто, а второе – правильная дробь, которую мы решать уже умеем.
После деления всегда желательно выполнять проверку.
В рассматриваемом примере можно привести к общему знаменателю  , и в результате получится в точности исходная неправильная дробь
, и в результате получится в точности исходная неправильная дробь 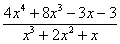
(2) От первого слагаемого сразу берем интеграл. Знаменатель дроби раскладываем на множители
Дальше всё идет по накатанной схеме:
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:


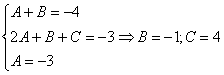
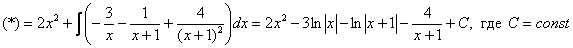
Готово.
И, наконец, заключительный пример для самостоятельного решения. Он очень интересен, рекомендую всем!
Пример 9
Найти неопределенный интеграл.
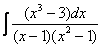
Только что обратил внимание, что во всех примерах урока в ходе решения систем у нас получались «хорошие» целые коэффициенты  . По той причине, что почти все интегралы я взял из сборника Рябушко. На практике же
. По той причине, что почти все интегралы я взял из сборника Рябушко. На практике же, когда автор методички придумает какой-нибудь корявый интеграл, часто будут появляться разные нехорошести.
Таким образом, если в ходе решения интеграла от дробно-рациональной функции у Вас получаются дробные значения коэффициентов  , то в этом нет ничего страшного, ситуация даже обыденна.
, то в этом нет ничего страшного, ситуация даже обыденна.
Желаю успехов!
Решения и ответы:
Пример 2: Решение:

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
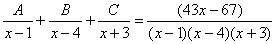
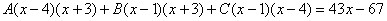
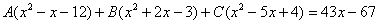
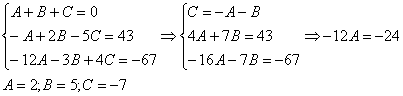
Комментарий: в правой части у нас нет слагаемого с 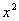 , поэтому в первом уравнении системы ставим справа ноль.
, поэтому в первом уравнении системы ставим справа ноль.
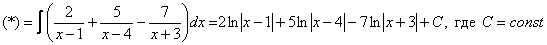
Пример 4: Решение:
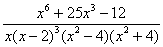
Шаг 1. Проверяем, правильная ли у нас дробь
Старшая степень числителя: 6
Старшая степень знаменателя: 8
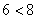 , значит, дробь является правильной.
, значит, дробь является правильной.
Шаг 2. Можно ли что-нибудь разложить в знаменателе на множители. Множитель 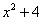 разложить нельзя, а вот
разложить нельзя, а вот 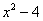 – можно:
– можно:
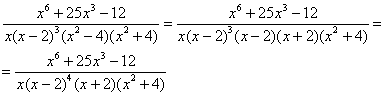
Шаг 3. Представим дробно-рациональную функцию в виде суммы элементарных дробей.
В данном случае, разложение имеет следующий вид:
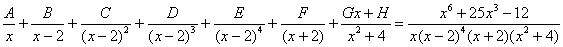
Пример 6: Решение:
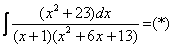
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
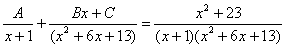

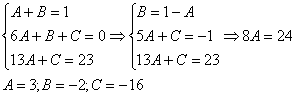

Пример 7: Решение:
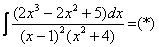
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
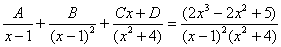



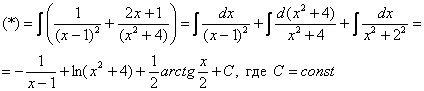
Пример 9: Решение:
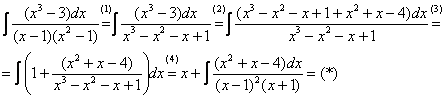
(1) Здесь неправильная дробь, поскольку старшие степени числителя и знаменателя равны: 3 = 3. Для того чтобы разделить числитель на знаменатель придётся временно раскрыть скобки в знаменателе.
(2)-(3) Теперь можно разделить 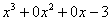 на знаменатель
на знаменатель 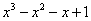 , но делать этого… я не буду. Можно поступить хитрее. Используем прием, который рассмотрен в первом параграфе урока Интегрирование некоторых дробей.
, но делать этого… я не буду. Можно поступить хитрее. Используем прием, который рассмотрен в первом параграфе урока Интегрирование некоторых дробей.
(4) От первого слагаемого сразу берем интеграл. Знаменатель оставшейся, уже правильной, дроби снова записываем в виде произведения множителей. Тут я немного подсократил разложение, надеюсь, всем понятно, что 
Далее накатанная колея…
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
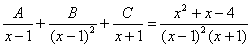
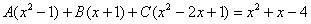
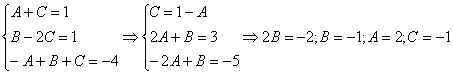
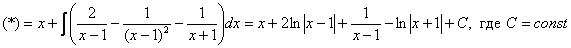
Вы выполнили проверку, мож где ошибочка вышла;)
Автор: Емелин Александр