
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Эквивалентные преобразования электрических цепей
|
|
 Если цепь с одним источником ЭДС включает в себя участки с только последовательным и параллельным соединением приемников, то расчет токов ветвей можно провести методом свертывания в следующей последовательности.
Если цепь с одним источником ЭДС включает в себя участки с только последовательным и параллельным соединением приемников, то расчет токов ветвей можно провести методом свертывания в следующей последовательности.
1. На схеме отмечаются все токи и узловые точки.
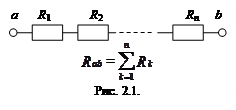
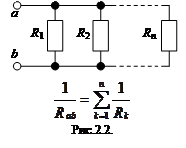 2. Группы резисторов с явно выраженным последовательным (рис. 2.1) или параллельным (рис. 2.2) соединением заменяются эквивалентными, и определяются их сопротивления.
2. Группы резисторов с явно выраженным последовательным (рис. 2.1) или параллельным (рис. 2.2) соединением заменяются эквивалентными, и определяются их сопротивления.
3. Замена производится до получения простейшей схемы, для которой элементарно определяется общее (эквивалентное) сопротивление всей цепи.
4. По заданному напряжению источника и вычисленному общему сопротивлению всей цепи определяется ток в неразветвленной части цепи (общий ток).
5. Определяются падения напряжения на участках цепи и ток каждого резистора.
Расчет цепи методом свертывания рассмотрим на следующем примере.

 Пример. В цепи (схема на рис. 2.3, а) сопротивления R 6 и R 7 заменим на R 67= R 6+ R 7 (рис. 2.3, б). Сопротивления R 5, R 6 и R 7 заменим на R 57=(R 5 R 67)/(R 5+ R 67) (рис. 2.3, в). Сопротивления R 4, R 5, R 6 и R 7 заменим на R 47= R 4+ R 57 (рис. 2.3, г). Сопротивления R 2 и R 47 заменим на R 247=(R 2 R 47)/(R 2+ R 47) (рис. 2.3, д). Наконец, найдем R экв= R 1+ R 3+ R 247.
Пример. В цепи (схема на рис. 2.3, а) сопротивления R 6 и R 7 заменим на R 67= R 6+ R 7 (рис. 2.3, б). Сопротивления R 5, R 6 и R 7 заменим на R 57=(R 5 R 67)/(R 5+ R 67) (рис. 2.3, в). Сопротивления R 4, R 5, R 6 и R 7 заменим на R 47= R 4+ R 57 (рис. 2.3, г). Сопротивления R 2 и R 47 заменим на R 247=(R 2 R 47)/(R 2+ R 47) (рис. 2.3, д). Наконец, найдем R экв= R 1+ R 3+ R 247.
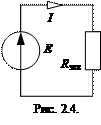
В получившейся цепи (рис. 2.4) найдем ток I в неразветвленной части цепи путем элементарного расчета по закону Ома для участка цепи. Для остальных схем, следуя в обратном порядке (от д к а) найдем напряжения на элементах по закону Ома и токи ветвей по первому закону Кирхгофа.
Расчет некоторых сложных электрических цепей значительно упрощается, если преобразовать треугольник сопротивлений в эквивалентную звезду или звезду сопротивлений в эквивалентный треугольник.
Контур, состоящий из трех сопротивлений RAB, RBC и RCA, имеющий три узловые точки A, B и C, образует треугольник сопротивлений (рис. 2.5, а).
Электрическая цепь, состоящая из трех сопротивлений RA, RB и RC, соединенных в одной узловой точке O, образует звезду сопротивлений (рис. 2.5, б).
Преобразование схемы должно производиться так, чтобы при неизменном напряжении между точками A, B и С токи IA, IB и IC звезды и треугольника оставались без изменений.
Треугольник и звезда, удовлетворяющие этому условию, называются эквивалентными.
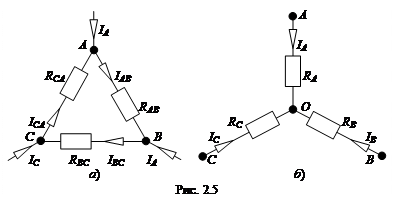
При замене треугольника эквивалентной звездой сопротивления звезды определяются следующими выражениями:

 При замене звезды эквивалентным треугольником каждое сопротивление треугольника определяется следующими выражениями:
При замене звезды эквивалентным треугольником каждое сопротивление треугольника определяется следующими выражениями:

Пример. Определить ток в неразветвленной части цепи (рис. 2.6, а) при следующих исходных данных: E =2, 2 В; R 1=10 Ом; R 2=30 Ом; R 3=60 Ом; R 4=4 Ом; R 5=22 Ом.
Решение. Для расчета этой цепи заменим треугольник сопротивлений, подключенных к точкам A, B и C, эквивалентной звездой, подключенной к тем же точкам (рис. 2.6, б).

Определим величины сопротивлений эквивалентной звезды:

Расчет сопротивления вновь полученной цепи производим методом свертывания.
Ra, 4, = Ra + R 4=6+4=10 Ом; Rc, 5= Rc + R 5=18+22=40 Ом.
Поскольку сопротивления между собой соединены параллельно, их общее сопротивление будет равно
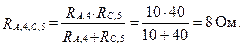
а общее сопротивление схемы (см. рис. 2.6, б) R = Rb + Ra, 4, c, 5=3+8=11 Ом. Тогда ток в неразветвленной части цепи I 0= E / R =2, 2/11=0, 2 А.