Понятие функции.

Тема 2.2. Числовая функция. Ее свойства и график.

Понятие функции.

Пусть рассматриваются два множества X и Y. Правило f, которое ставит в соответствие каждому x∈ X единственный элемент y∈ Y, назовем функцией, заданной на множестве X и принимающей значения на множестве Y.

Функция – правило f, которое каждому элементу x∈ X ставит в соответствие единственный элемент y∈ Y. При этом используют запись у = f(x).

Слово «функция» образовано от латинского functio, что означает исполнение, осуществление.

Переменную х называют независимой переменной или аргументом, а переменную у – зависимой переменной. Говорят, что у является функцией от х.

Значение у, соответствующее заданному значению х, называют значением функции.

Все значения, которые принимает независимая переменная, образуют область определения функции; все значения, которые принимает зависимая переменная, образуют множество значений функции.

Для функции f приняты обозначения: D(f) – область определения функции, E(f) – множество значений функции, f(x₀) – значение функции в точке х_{0 .}

Есл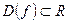и и 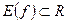, то функцию называют числовой.

Элементы множества 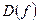так же называют значениями аргумента, а соответствующие им элементы 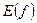– значениями функции.