Способы задания функции.

1) Аналитический способ. Функция задается в виде формулы 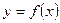, где переменная - элемент множества значений аргумента, а переменная 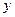- соответствующее значение функции.

Если функция задана формулой и область определения функции не указана, то считают, что область определения состоит из всех значений независимой переменной, при которых эта формула имеет смысл.

2) Табличный способ. Функция 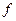полностью определяется заданием множества пар 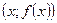, где принимает все значения из 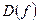, а 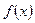- соответствующие значения функции. Способ применяется в тех случаях, когда область определения функции дискретна (состоит из конечного числа значений). В виде таблиц записывают результаты экспериментального исследования каких-либо процессов.

3) Функция может быть задана графически.

Графиком функции 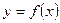называется изображение на координатной плоскости множества пар .

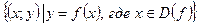График дает наглядное представление о функции, поэтому часто используется в процессе ее исследования.

Заметим, однако, что не всякое множество точек координатной плоскости является графиком некоторой функции. Например на кривой, изображенной на рис., значению 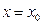соответствуют три значения 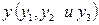, и, следовательно, такое соответствие не является функцией.

Для того, чтобы множество точек координатной плоскости являлось графиком некоторой функции, необходимо и достаточно, чтобы любая прямая, параллельная оси Оу, пересекалась с указанным графиком не более чем в одной точке.

Пример 1. Найти область определения функции: а) 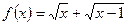; б) .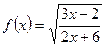

Решение.

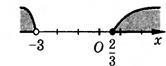
а) : .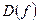

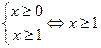б) 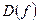: