Свойства числовых функций.

Монотонность.

1. Функция 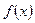называется возрастающей на данном числовом промежутке 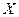, если большему значению аргумента 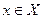соответствует большее значение функции 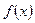, т.е. для любых 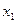и 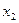из промежутка 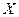, таких что 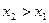, выполнено неравенство .

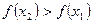2. Функция 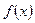называется убывающей на данном числовом промежутке 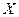, если большему значению аргумента 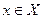соответствует меньшее значение функции 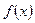, т.е. для любых 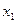и 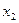из промежутка 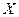, таких что 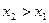, выполнено неравенство .

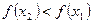3. Функция только убывающая или только возрастающая не данном числовом промежутке, называется монотонной на этом промежутке.

4. Теорема (о корне). Пусть функция 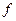возрастает (убывает) на промежутке 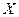, число а - любое из значений, приеимаемых 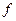на этом промежутке. Тогда уравнение 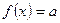имеет единственный корень в промежутке .

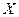Четные и нечетные функции.

1. Функция 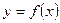называется четной, если она обладает следующими двумя свойствами:

1) область определения этой функции симметрична относительно начала координат (т.е. если точка а принадлежит области определения, то точка –а также принадлежит области определения);

2) для любого значения , принадлежащего области определения этой функции, выполняется равенство .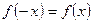

2. Функция 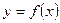называется нечетной, если она обладает следующими двумя свойствами:

1) область определения этой функции симметрична относительно начала координат;

2) для любого значения , принадлежащего области определения этой функции, выполняется равенство .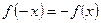

Например, четными являются функции 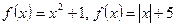определенные на всей числовой прямой, и функция 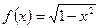, определенная на отрезке 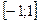; нечетными являются функции 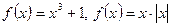, определенные на всей числовой прямой, и функция 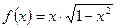, определенная на отрезке .

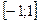Функции, которые не являются ни четными, ни нечетными, называются функциями общего вида. Например, .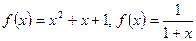

Пример2. Выяснить четность или нечетность функции:

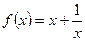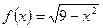а) ; б) ; в) .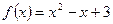

Решение:

а) Дана функция 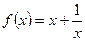, где 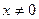. Найдем :

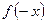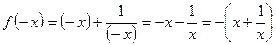.Получили 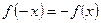, следовательно 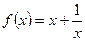- функция нечетная.

б) Дана функция 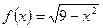, 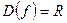. Переменим знак у аргумента функции 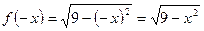. Получили 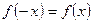, следовательно 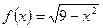- функция четная.

в) Дана функция 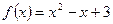, 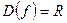. Переменим знак у аргумента функции и упростим: 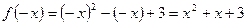. Получили 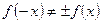, следовательно 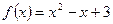- функция общего вида.

Периодические функции.

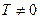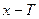1.Функция называется периодической, если существует такое число , что при любом из области определения функции числа и 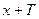также принадлежат этой области и выполняется равенство 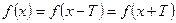.В этом случае число 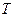называется периодом функции .

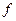2.Если 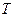- период функции, то 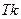, где 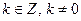, также период функции. Следовательно, всякая периодическая функция имеет бесконечное множество периодов.На практике обычно рассматривают наименьший положительный период.

3.Значения периодической функции через промежуток, равный периоду, повторяются. Это обстоятельство используется при построении графиков.

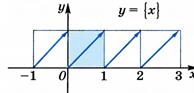
Промежутки знакопостоянстваи корни функции.

1.Числовые промежутки, на которых функция сохраняет свой знак (т.е. остается положительной или отрицательной), называются промежутками знакопостоянства функции.

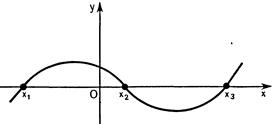
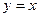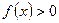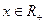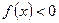2.О промежутках знакопостоянства функции легко судить по ее графику. Рассмотрим, например, функцию .Здесь при , при 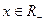. В первом случае график расположен выше оси Ох, во втором – ниже ее.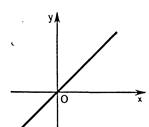

3.Значения аргумента 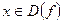, при которых 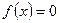, называются корнями (или нулями) функции.Значения аргумента, при которых функция обращается в нуль – это абсциссы точек пересечения графика функции с осью Ох.