
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод замены плоскостей
|
|
Сущность этого метода заключается в том, что положение точек, линий, плоских фигур, поверхностей в пространстве остается неизменным, а система плоскостей П1 П2 дополняется плоскостями, образующими с П1 или П2 или между собой системы двух взаимно перпендикулярных плоскостей, принимаемых за плоскости проекций.
Каждая новая система выбирается так, чтобы получить положение, наиболее удобное для выполнения требуемого построения.
На рисунке 37 показано построение натуральной величины отрезка прямой АВ и угла ее наклона к плоскости П1 – α методом замены плоскостей. Для этого в систему плоскостей П1 П2 введена дополнительная плоскость П4 так, чтобы она была параллельна плоскости П1 (ось П1/П4 перпендикулярна горизонтальной проекции прямой А1В1). Проекция отрезка на эту плоскость А4В4 является натуральной величиной отрезка АВ и показывает угол наклона его к плоскости П1.
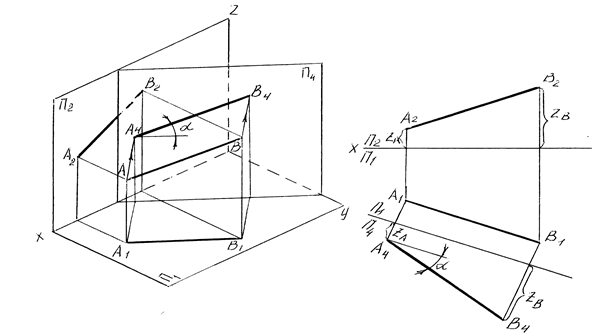
а б
Рисунок 37 – Определение натуральной величины отрезка методом замены плоскостей проекций
а – наглядное изображение, б – комплексный чертеж
На рисунке 38 решена задача по определению натуральной величины расстояния от точки до плоскости Р, заданной следами.
Введение дополнительной плоскости П4 перпендикулярно горизонтальному следу плоскости Р1, дает возможность преобразовать плоскость Р таким образом, чтобы она заняла фронтально-проецирующее положение. Для этого на фронтальном следе плоскости Р2 выбирают произвольную точку N и строят ее проекцию на плоскость П4. Затем через проекцию точки N4 и точку пересечения следа Р1 с осью П1/П4 проводят след плоскости Р4. Строят проекцию точки А на плоскость П4 и, опустив из нее перпендикуляр на след плоскости Р4, определяют расстояние от точки А до плоскости Р.

Рисунок 38 – Определение расстояния от точки до плоскости методом замены плоскостей проекций
Метод вращения. Он состоит в том, что заданная система плоскостей проекций остается неизменной, а фигуру вращают вокруг неподвижной оси до тех пор, пока она не займет частное положение, т.е. станет параллельной или перпендикулярной одной из плоскостей проекций. Вращение осуществляют вокруг осей, перпендикулярных или параллельных плоскостям проекций.
На рисунке 39 показан поворот точки вокруг оси, перпендикулярной плоскости проекций П2. При вращении точки вокруг этой оси фронтальная проекция точки перемещается по окружности, а горизонтальная – по прямой, перпендикулярной к проекции оси вращения.

Рисунок 39 – Метод вращения
При повороте отрезка вокруг оси, перпендикулярной к плоскости П1, величина его горизонтальной проекции не изменяется (рисунок 40а).
При повороте отрезка вокруг оси, перпендикулярной к плоскости П2, величина его фронтальной проекции не изменяется (рисунок 40б).
а б
Рисунок 40 – Вращение отрезка вокруг оси, перпендикулярной к
а – плоскости П1, б – к плоскости П2
Частным случаем метода вращения является метод плоско-параллельного перемещения. При плоскопараллельном перемещении элемента в пространстве все его точки перемещаются в плоскостях, параллельных между собой. Этот метод может рассматриваться как вращение без указания осей вращения.
Если элемент совершает плоскопараллельное перемещение относительно плоскости П1, то фронтальные проекции его точек будут перемещаться по прямым, перпендикулярным к линиям связи. Горизонтальная проекция перемещающегося элемента при этом, изменяя свое положение, остается равной самой себе.
В случае плоскопараллельного перемещения элемента относительно плоскости проекций П2, горизонтальные проекции его точек двигаются по прямым, перпендикулярным линиям связи, а фронтальная проекция элемента, изменяя свое положение в соответствии с заданным условием, остается равной себе.
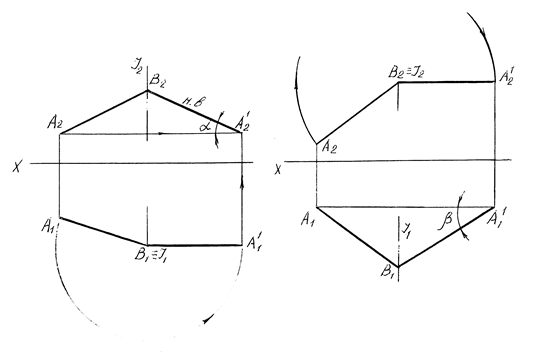
На рисунке 41 показан пример построения натуральной величины отрезка прямой АВ и углов его наклона к плоскостям проекций. Для определения угла наклона отрезка к плоскости проекций П1(α), поворачиваем отрезок таким образом, чтобы он занял положение, параллельное плоскости П2. При таком повороте горизонтальная проекция отрезка не изменяет своей величины, поэтому берем проекцию А1В1 и располагаем параллельно оси X. Фронтальную проекцию находим по линиям связи. Отмечаем угол α и натуральную величину отрезка. Аналогично строим угол наклона прямой к плоскости проекций П2(β), при этом поворачиваем отрезок АВ таким образом, чтобы он занял положение, параллельное плоскости проекций П1.

Рисунок 41 – Построение натуральной величины отрезка АВ и углов наклона его к плоскостям проекций методом плоскопараллельного перемещения
На рисунке 42 приведен пример определения расстояния от точки А до плоскости Р, заданной следами. Для решения этой задачи методом плоскопараллельного перемещения необходимо повернуть плоскость Р таким образом, чтобы она заняла проецирующее положение. Задача решается в следующей последовательности:
- проводим в плоскости Р произвольную горизонталь (фронталь) через точку N;
- поворачиваем горизонталь (фронталь) и след плоскости Р1 таким образом, чтобы расстояние между ними не изменилось и они заняли положение, перпендикулярное оси Х. Вместе с плоскостью поворачиваем точку А;
- строим фронтальную проекцию горизонтали (точка N21) и через нее проводим след плоскости Р21;
- расстояние от точки до плоскости определяется как перпендикуляр, опущенный из точки на плоскость Р.

Рисунок 42 – Определение расстояния от точки до плоскости методом плоскопараллельного перемещения