
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Представление синусоидальных функций в различных формах.
|
|
 1.Аналитическое(с пом. формул): i(t)= Imsin(wt+j); (т.ж. для u, e).2.Графически(см.выше)
1.Аналитическое(с пом. формул): i(t)= Imsin(wt+j); (т.ж. для u, e).2.Графически(см.выше)
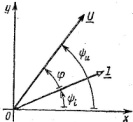
3. при помощи векторов. длина вект д.б = амплит тока, напряж, эдс, а угол наклоа к оси абцисс показ нач фазу.
u(0)=Umsinwt, i(0)=Imsinwt – без нач сдвига фаз. u(t)=Umsin(wt+ju), i(t)= Imsin(wt+ji) – с нач сдв.
 Вектора изобр. неподвижными.Углы накл. к оси абсцисс = нач. фазам.Угол сдвига фаз φ =φ u-φ i. Если φ u> φ i, товектор u опер. i.на угол φ. и наоборот! угол φ всегда откл. от вектора тока к вект напр. Собокупность векторов(e, I, u)изобр.в общей сист.коорд наз. вект. диагр.
Вектора изобр. неподвижными.Углы накл. к оси абсцисс = нач. фазам.Угол сдвига фаз φ =φ u-φ i. Если φ u> φ i, товектор u опер. i.на угол φ. и наоборот! угол φ всегда откл. от вектора тока к вект напр. Собокупность векторов(e, I, u)изобр.в общей сист.коорд наз. вект. диагр.
4. при помощи комплекс. чисел..
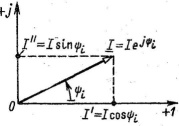
+1 –ось действ.чисел; +j – мнимые числа().
I·=I’+I”-алг.форма записи, где I’=Icosφ, I”=Isinφ.
I =Icosj+jIsinj - тригон форма записи.
Ф-ла Эйлер: ejj=cosj+jsinj. I =Iejj-показат-я форма
Переход от алг формы к тригоном: I=Ö (I’2+I”2), j=arctg(I”/I’)при I”> 0; j=arctg(I”/I’+180)при I”< 0.
4. цепь перемен тока с резистором. Вектор диагр. з.Ома в компл форме.
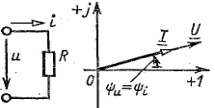 Если к резитив эл-ту приложено синусоид напряж, то по з-ну Ома для мгнов знач i=u/R= Umsin(wt+ju)/R. => ток измен по синусоид з-ну.
Если к резитив эл-ту приложено синусоид напряж, то по з-ну Ома для мгнов знач i=u/R= Umsin(wt+ju)/R. => ток измен по синусоид з-ну.
Нач фаза тока ji =ju, => сдвиг фаз j=ju-ji =0, т.е напряж и ток совп по фазе.
Заменим мгнов знач комплек выр-ми: 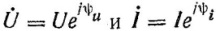 , разделим U на I:
, разделим U на I: 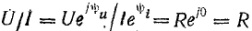
З-н Ома в компл форме: I=U/R
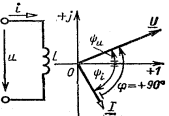
5.Цепь перемен тока с индуктив эл-том. Вектор диагр.
 Синусоид ток в индуктив эл-те: i= Imsin(wt+ji);, Im=Um, /ω L – амплитуда тока, I=U, /ω L – действующее знач, где ω L=XL - индукт сопротив.
Синусоид ток в индуктив эл-те: i= Imsin(wt+ji);, Im=Um, /ω L – амплитуда тока, I=U, /ω L – действующее знач, где ω L=XL - индукт сопротив.
Угол сдвига фаз м/д напряж и током j=ju-ji =90 (график)
Разделим напряж на ток: 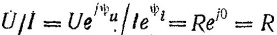 . З-н ома в компл форме: I=U/jXL.
. З-н ома в компл форме: I=U/jXL.
6. Цепь перемен тока с емк эл-том. Вектор диагр.
 ток на участке цепи с емк эл-том при синусоид напряж также синусоидален:
ток на участке цепи с емк эл-том при синусоид напряж также синусоидален:
i= Imsin(wt+ji).
Ампл тока Im=Umω С, а его действующ знач I=Uω С. Велич, обратная ω С, наз емк сопротивл: ХС=1/ω С
Угол сдвига фаз м/д напр и током: j=ju-ji = -90(график)
З-н ома в компл форме: I=U/Х-jXС
7. Р =ем sin (ω t-240)
езонанс напряж. Вектор диагр.Резонанс токов. Вект. диагр.
Рез-с – режим участка цепи, содержащий индук и емкос эл-ты, при к-м разность фаз напр-я и тока участка=0.
Виды: 1. Рез напряж – возможен на уч-ке цепи с послед соед R, L и CПри рез-се
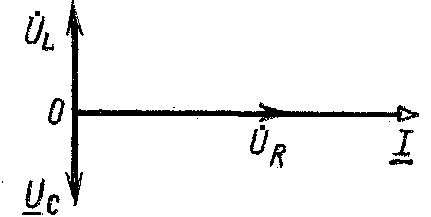
Условия рез-са: XL=XC.
Изменение частоты, инд-ти, емкости.
ω =1/Ö LС=ω 0, ω 0 – рез-я частота.
Особ-ти режима рез-са напр: 1. j=0, то cosφ =1 и суммар сопротивл участка цепи активное. Zрез=Ö R2+(XL-XC)2=R, т.е.сопр. мин-но. 2.Ток Iрез=U/Zрез=U/R максимален. 3.Напряж на отдел уч-ках контура: UR=RIрез; UL=XLIрез; UC=XCIрез. 4.Актив мощ-ть при резонансе макс, т.к Р=RI2рез, а ток – макс.
В силовых цепях при резонансе XL=XC.> R, т.е. UL=UC.> Ur, это опасно
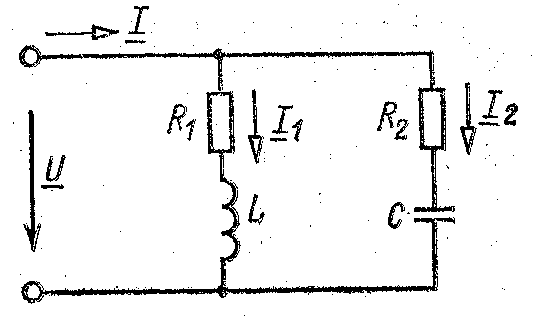
2. Рез токов – возможен в цепи с парал соед двух ветвей с параметрами R1, L и R2, C в параллел контуре.
Особ-ти: 1. j=0, cosφ =1 и общее сопротив контура активное, то полная проводим-ть контура = актив провод-ти и практич миним-на. 2.Ток в незазветвл части цепи практич миним. 3. Реактив составл-щие токов равны и Iр=Iр1+Iр2=0. Ток в общей цепи=актив составляющей тока.
4.Реактив мощ-ти QL=QC, т.к QL=BLU2, QC=BCU2.
8. цепь перемен тока с послед соед эл-тов. З-ны ома и К-фа в компл форме и для мгнов знач. С параллельн. соединением.
Если к участку с послед соед эл-тов R, L и C приложено синусоид напряж, то ток в цепи синусоид-е. Положительное значение тока выбирается произвольно. 1з.К.: Алг. сумма мгнов.значений токов в узле равна нулю.На кажд из эл-тов будет падать напряж, причем по 2 з-ну К-фа для мгнов знач u=uR+uL+uC. Заменим мгнов знач комплекс выр-ми: U=UR+UL+UC. … U=RI+jXL-JxCI.».з.К.: Алг. сумма напряж. на резестивных, инд-х и емкостных эл-х контура в данный момент времени равна алг. сумме ЭДС в том же контуре в тот же мом. времени.
З-н ома в комплекс форме: I=U/[R+j(XL-XC)].