Уравнение плоскости.

НЕДЕЛЯ 4

Лекция 4

Пусть заданы прямоугольная система координат Oxyz, произвольная плоскость П, точка 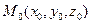и вектор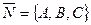

Уравнение

(1)

определяет плоскость, проходящую через точку 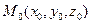перпендикулярно вектору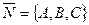

В уравнении (1) раскроем скобки

.

Выражение, стоящее в скобках обозначаем через Д, тогда получим

(2)

Уравнение (2) называется общим уравнением плоскости. Вектор 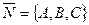называется нормальным вектором плоскости.

Если в общем, уравнении плоскости коэффициент 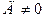то, разделив все члены уравнения на – Д, уравнение плоскости можно привести к виду

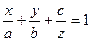(3)

здесь Это уравнением плоскости в «отрезках» в нем а, b и с соответствует абсциссе, ординате и аппликате точек пересечения плоскости с осями координат О_х, О_у, О_z.

При любом расположении (2) плоскостей П₁, П₂

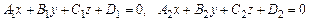(4)

в пространстве один из углов 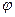между ними равен углу между их нормальными векторами и вычисляется по формуле

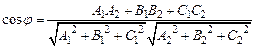(5)

Если два уравнения (4) определяют одну и ту же плоскость, то их коэффициенты пропорциональны

(6)

Если плоскости П₁ и П₂ параллельны, то коллениарны их нормальные векторы 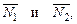и наоборот. Но тогда

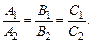(7)

Условие (7) является условием параллельности плоскостей.

Если же плоскости П₁ и П₂ перпендикулярны, то перпендикулярны их нормальные векторы 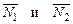. Но тогда их скалярное произведение равно 0, т.е.

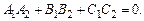(8)

Равенство (8) определяет условие перпендикулярности плоскостей.