И плоскости в пространстве.

Прямая в пространстве может быть задана системой уравнений двух плоскостей

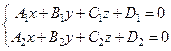, (1)

пересекающихся по этой прямой.

Уравнения (1) называются общими уравнениями прямой. Для решения задач уравнения (1) не всегда удобны, по этому используют специальный вид уравнения прямой.

Пусть дана прямая L и ненулевой вектор 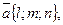лежащий на данной прямойили параллельно ей. На прямой L возьмем точку M 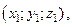тогда уравнение этой прямой можно записать следующим образом

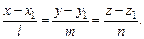(2)

Уравнение (2) называется каноническим уравнением прямой.

От канонических уравнений прямой, введя параметр легко можно перейти к параметрическим уравнением:

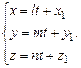(3)

Пусть заданы две прямые каноническими уравнениям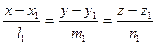и.

и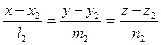

При любом расположении этих прямых в пространстве, один из двух углов между ними равен углу 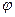между их направляющими векторами 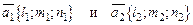. Угол 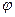можно вычислить по формуле

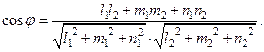(4)

Условие параллельности и перпендикулярности двух прямых в пространстве имеют следующий вид

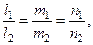(5)

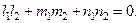(6)

Рассмотрим теперь взаимное расположение прямой 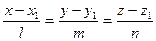и плоскости Ax+By+C z+ D=0.

Угол между прямой и плоскостью определяется по формуле

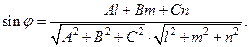(7)

Условием параллельности прямой и плоскости является условие

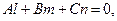(8)

а условием перпендикулярности прямой и плоскости

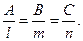
Литература: К.А. Хасеинов Каноны математики. Стр.96-110.

(9)