
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Поверхности второго порядка
|
|
Общее уравнение второй степени с тремя переменными
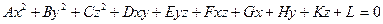
может определять в пространстве некоторую поверхность, называемую поверхностью второго порядка. С помощью преобразования системы координат уравнение такой поверхности может быть приведено к каноническому (простейшему) виду. Укажем различные типы поверхностей, описываемые каноническими уравнениями.
1. Сфера.
Множество точек пространства, равноудаленных от данной точки, называемой центром, называется сферой.
Уравнение сферы имеет вид
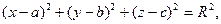
где С(a, b, c) – центр сферы, R- радиус сферы. Если центр сферы расположен в начале координат, то уравнение сферы принимает вид
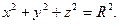
2. Цилиндрические поверхности.
Цилиндрической поверхностью называется поверхность, составленная из всех прямых, пересекающих данную линию L и параллельных данной прямой l. При этом линия L называется направляющей цилиндрической поверхности, а каждая из прямых, составляющих эту поверхность и параллельных прямой l – образующей. Укажем уравнения цилиндрических поверхностей для случаев, когда направляющие лежат в одной из координатных плоскостей, а образующие параллельны координатной оси, перпендикулярной этой поверхности.
Уравнение вида F(x, y)= 0 в пространстве определяет цилиндрическую поверхность с образующими, параллельными оси Оz. Аналогично, уравнение
F(x, z)= 0 определяет цилиндрическую поверхность с образующими, параллельными оси Оy, и F(y, z) - цилиндрическую поверхность с образующими, параллельными оси Ох.
Канонические (простейшие) уравнения цилиндрических поверхностей второго порядка
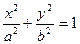 - эллиптический цилиндр;
- эллиптический цилиндр;
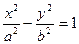 - гиперболический цилиндр;
- гиперболический цилиндр;
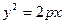 - параболический цилиндр.
- параболический цилиндр.
Уравнения всех трех цилиндров с образующими, параллельными оси Оz, не содержат координаты z и совпадают с уравнениями направляющих, определяющих кривые второго порядка, соответственно эллипс, гиперболу и параболу, лежащих в плоскости Оху.
3. Конические поверхности.
Конической поверхностью называется поверхность, составленная всеми прямыми, пересекающими данную линию L и проходящими через данную точку Р. Линия L называется направляющей конической поверхности, точка Р – ее вершиной, а каждая из прямых, составляющих коническую поверхность, - образующей.
Пусть направляющей конической поверхности с вершиной в начале координат является эллипс

тогда можно получить уравнение конической поверхности в виде
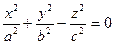 ,
,
которое называется конус второго порядка.
4. Эллипсоид.
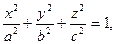
а, b, c – полуоси эллипсоида.
5. Однополостной гиперболоид.
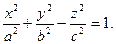
6. Двуполостной гиперболоид.
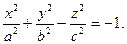
6. Эллиптический параболоид.
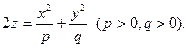
7. Гиперболический параболоид.

Литература: К.А. Хасеинов Каноны математики. Стр.110-120.