Односторонние пределы функции

НЕДЕЛЯ 6

Лекция 11

Функция. Предел функции.

Односторонние пределы функции

Пусть функция у=f(х) определена в некоторой окрестности точки х ₀. Тогда число А называется пределомфункции у = f (х) при х х ₀ (в точке х = х ₀), если для любого 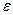> 0 существует 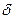= 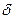(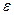)> 0, такое, что при 0 < | х—х ₀|< 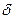справедливо неравенство | f (х)- А |< .

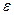Если А – предел функции f (х) при х х ₀, то записывают это так

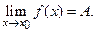
В самой точке х ₀функция f (х)может и не существовать (f (х ₀) не опре­делено). Аналогично запись 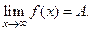обозначает, что для любого 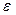> 0 существует N = N (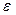)> 0, такое, что при | х|> N выполняется неравенство | f (х) -А| < .

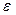Если существует предел вида 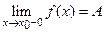, который обозначают также 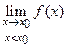или f (х ₀ - 0), то он называется пределом слева функции f (х)в точке x ₀. Аналогично если существует предел вида 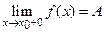(в другой записи 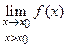или f (x ₀+0)), то он называется пределом справафункции f (х)в точке x ₀. Пределы слева и справа называются односто­ронними. Для существования предела функции f(х)в точке x ₀необходимо и достаточно, чтобы оба односторонних предела в точке x ₀существовали и были равны, то есть f (x ₀-0)=f(x ₀+0).