
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Широко используются следующие два предела
|
|
1) 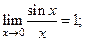
2) 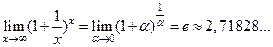 ,
,
которые называются соответственно первым и вторым замечательными пределами.
Если 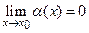 (т. Е. для любого
(т. Е. для любого 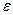 > 0 существует число
> 0 существует число 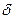 > 0, такое что при 0<
> 0, такое что при 0< 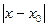 <
< 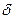 справедливо неравенство
справедливо неравенство 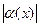 <
< 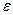 ), то
), то  называется бесконечно малойфункцией или величиной при х
называется бесконечно малойфункцией или величиной при х 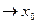 .
.
Для сравнения двух бесконечно малых функций  и
и 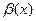 при х
при х 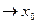 находят предел их отношения
находят предел их отношения
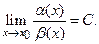 (1)
(1)
Если С  0, то
0, то  и
и 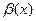 называются бесконечно малыми величинами одного и того же порядка; если С =0, то
называются бесконечно малыми величинами одного и того же порядка; если С =0, то  называется бесконечно малой более высокого порядка по сравнению с
называется бесконечно малой более высокого порядка по сравнению с 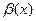 , а
, а 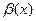 - бесконечно малой более низкого порядка по сравнению с
- бесконечно малой более низкого порядка по сравнению с  .
.
Если 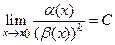 (0<
(0< 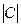 <
<  ),
),  то
то  называется бесконечно малойпорядка k, по сравнению с
называется бесконечно малойпорядка k, по сравнению с 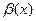 при х
при х 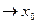 .
.
Если 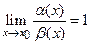 , то бесконечно малые
, то бесконечно малые  и
и 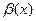 при х
при х 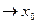 называются эквивалентными(равносильными) величинами и обозначают
называются эквивалентными(равносильными) величинами и обозначают  ~
~ 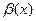 .
.
Например, при х 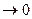
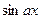 ~
~ 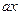 ,
, 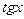 ~ х,
~ х,  ~ х,
~ х, 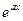 — 1~
— 1~ 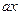 ..
..
Легко доказать, что предел отношения бесконечно малых функций  и
и 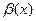 при х
при х 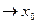 равен пределу отношения эквивалентных им бесконечно малых функций
равен пределу отношения эквивалентных им бесконечно малых функций 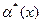 и
и 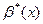 при х
при х 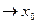 , т.е. верны предельные равенства
, т.е. верны предельные равенства
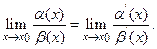
Литература: К.А. Хасеинов Каноны математики. Стр.130--146.
Лекция 12