Определение приведенных моментов инерции механизма.

Для звена, совершающего поступательное движение (ползун), кинетическая энергия

,

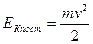где m– масса звена;

v- скорость поступательного движения

Для звена, совершающего вращательное движение (кривошип, коромысло), кинетическая энергия

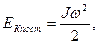
где J– момент инерции относительно оси вращения;

w – угловая скорость звена.

Кинетическая энергия звена, совершающего сложное плоскопараллельное движение

,

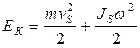где v _S – скорость центра масс звена;

J_S –момент инерции звена относительно оси, проходящей через центр масс.

Складывая кинетические энергии всех звеньев, получим полную кинетическую энергию механизма.

В нашем примере полная кинетическая энергия механизма

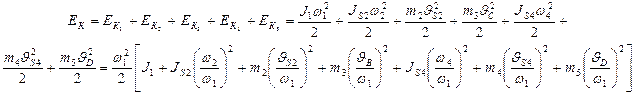
Выражение в квадратных скобках представляет собой приведенный к начальному звену момент инерции механизма.

Вычислим приведенный момент инерции для 12-ти положений механизма.

Для 2-го положения механизма

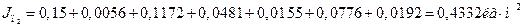
Вычисления приведенного момента инерции для остальных положений механизма сводим в таблицу 3.2.

По данным таблицы строим диаграмму приведенного момента инерции механизма в функции угла поворота начального звена. Принимаем масштаб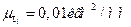

Методом исключения общего параметра j из диаграмм 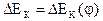и 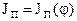строим диаграмму энергомасс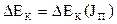

Таблица 3.2-Результаты расчета приведенного момента инерции механизма

№
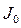
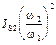
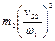
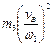
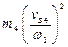
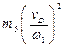
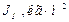
	0, 15	0, 0207	0, 0552			0, 1219	0, 0463	0, 3941
	0, 15	0, 0155	0, 0776	0, 0192	0, 0056	0, 1172	0, 0481	0, 4332
	0, 15	0, 0056	0, 1172	0, 0481	0, 0155	0, 0776	0, 0192	0, 4332
	0, 15		0, 1219	0, 0463	0, 0207			0, 3389
	0, 15	0, 0056	0, 0933	0, 0241	0, 0155	0, 0776	0, 0192	0, 3889
	0, 15	0, 0155	0, 0686	0, 0062	0, 0056	0, 1172	0, 0481	0, 3853
	0, 15	0, 0207	0, 0552			0, 1219	0, 0463	0, 4112
	0, 15	0, 0155	0, 0686	0, 0062	0, 0056	0, 0954	0, 0241	0, 3941
	0, 15	0, 0056	0, 0933	0, 0241	0, 0155	0, 0617	0, 0062	0, 3654
	0, 15		0, 1219	0, 0463	0, 0207			0, 3389
	0, 15	0, 0056	0, 1172	0, 0481	0, 0155	0, 0617	0, 0062	0, 4043
	0, 15	0, 0155	0, 0776	0, 0192	0, 0056	0, 0954	0, 0241	0, 3874

По данному коэффициенту неравномерности движения d=1/95 и средней угловой скорости 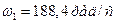определяем углы y_max. и y_min, образуемые касательными к диаграмме энергомасс с осью абсцисс,

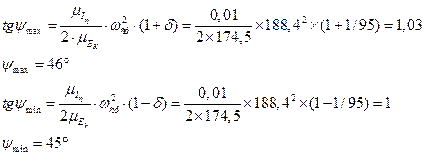
Построив стороны этих углов и перенеся их параллельно самим себе до момента касания с кривой энергомасс соответственно сверху и снизу, получим на оси DE_К отрезок mn, заключенный между этими касательными.

По отрезку mn определяем момент инерции маховика

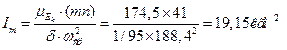
Диаметр маховика, выполненного в виде сплошного диска, определяется по формуле:

,

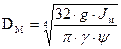где 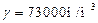- удельный вес материала маховика (чугун);

y=0, 1. Тогда

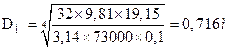
Маховой момент 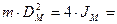кгм²

Тогда масса маховика

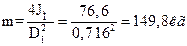
а ширина обода

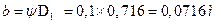
4. ПРОЕКТИРОВАНИЕ КУЛАЧКОВОГО МЕХАНИЗМА

Широкое применение кулачковых механизмов обусловлено тем, что с их помощью легко воспроизводится заданный закон движения ведомого звена.

Нужно иметь в виду, что при выборе закона движения ведомого звена могут возникнуть удары в кулачковом механизме. Различают следующие группы законов движения: с жесткими ударами, с мягкими ударами, без ударов. Жесткие удары в кулачковом механизме имеют место, когда подъем или опускание толкателя происходит с постоянной скоростью. При синусоидальном законе движение происходит без жестких и мягких ударов (этот закон рекомендуется при проектировании быстроходных кулачковых механизмов).

Для синтеза (проектирования) кулачкового механизма задаются: схема механизма; максимальное линейное h или угловое y перемещение ведомого звена; фазовые углы поворота кулачка (удаления - j_у, дальнего стояния j_{д.с .}, возвращения j_в); законы движения выходного звена для фазы удаления и возвращения; длина коромысла l для коромысловых кулачковых механизмов. Исходя из условий ограничения угла давления, определяют основные размеры звеньев кулачкового механизма; минимальный радиус кулачка, положение коромысла относительно центра вращения кулачка, проектируют профиль кулачка графическим или аналитическим методами.