Построение профиля кулачка коромыслового кулачкового механизма.

Главным этапом синтеза кулачкового механизма является построение профиля кулачка, в основу которого положен метод обращенного движения. Суть этого метода заключается в том, что всем звеньям механизма условно сообщается дополнительное вращение с угловой скоростью, равной угловой скорости кулачка, направленной в обратную сторону. Тогда кулачок остановится, а стойка вместе с коромыслом придет во вращательное движение вокруг центра кулачка О с угловой скоростью – w_к. Кроме того, толкатель будет совершать ещё движение относительно стойки по закону, который определяется профилем кулачка.

Из центра О проводим окружности радиусами r_min и l_АВ. Определяем положение центра ролика коромысла, для чего из точки А радиусом, равным длине коромысла, проводим дугу до пересечения с окружностью радиуса r_min. Точка пересечения В₀ и есть положение центра ролика коромысла, соответствующее началу удаления. На траекторию точки В коромысла наносим разметку её согласно диаграмме S(j). Получаем точки В₁, В₂, В₃…В_6.

Для определения действительного профиля кулачка необходимо определить радиус ролика. Радиус ролика должен быть меньше максимального радиуса кривизны r_min центрового (теоретического) профиля кулачка:

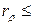(0, 7¸ 0, 8) r_min

Из конструктивных соображений радиус ролика не рекомендуется принимать больше половины минимального радиуса:

r_p £ (0, 4 ¸ 0, 5)r_min

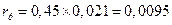м

Принимаем r_p равным 9 мм.

Действительный (практический) профиль кулачка получим, если построим эквидистантную кривую радиусом, равным r_{p .}

5. ПРОЕКТИРОВАНИЕ ЭВОЛЬВЕНТНОГО

ЗАЦЕПЛЕНИЯ ПРЯМОЗУБЫХ ЦИЛИНДРИЧЕСКИХ КОЛЁС

Принимаем, что зубчатые колеса изготовлены без смещения исходного контура (X₁=X₂ =0). Тогда угол зацепления равен углу профиля инструмента (a_w = a =20°), делительные окружности являются одновременно начальными окружностями зацепления (r_w1 = r₁ и r_w2 = r₂). Рассчитываемая зубчатая передача имеет следующие параметры:

Z₁ = 20; Z₂ = 15; m = 9 мм

Радиусы начальных окружностей колес

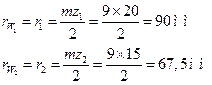
Радиусы основных окружностей колес

;

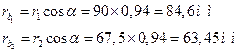Радиусы окружностей вершин зубьев

;

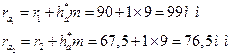где 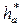=1 – коэффициент высоты головки зуба, а 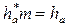– высота головки зуба (расстояние, измеренное по радиусу между делительной окружностью и окружностью вершин).

Радиусы окружностей впадин колес

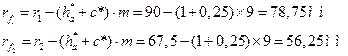
где с^*= 0, 25 – коэффициент радиального зазора;

с=c*m – радиальный зазор, мм.

Шаг по делительной окружности

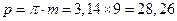мм

Окружная толщина зуба по делительной окружности

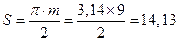мм

Межосевое расстояние

a_w = a = r_w1+r_w2 = 90+67, 5=157, 5 мм

где a=r₁+r₂ - делительное межосевое расстояние, мм.

Высота зуба определяется как

h=h_a+h_f=h*_a× m+(h*_а+с*)× m =1 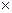9+(1+0, 25) 9=20, 25 мм,

h= 2, 25m =2, 25 × 9 = 20, 25 мм.

Для построения профилей зацепления зубчатых колес выбираем масштаб 2: 1, значит на чертеже все полученные значения величин увеличиться в 2 раза.

Построение профилей зубьев проводим в следующем порядке:

- откладываем межосевое расстояние a_w (O₁O₂ на чертеже);

- Радиусами r_w1 и r_w2 проводим начальные окружности колес. Точка P касания их является полюсом зацепления;

- проводим основные окружности колес, окружности вершин зубьев и окружности впадин;

- через полюс зацепления P проводим общую касательную t-t к начальным окружностям колес и линию зацепления n-n, касающуюся в точках A и B основных окружностей. Часть ab линии n-n, заключенная между окружностями вершин зубьев, называется активной линией зацепления, т.е. геометрическим местом действительного касания профилей зубьев;

- строим эвольвенты профилей зубьев, соприкасающихся в полюсе зацепления P. Профили зубьев получают обкатывая линию зацепления как по одной, так и по другой основным окружностям. При обкатывании точка P линии зацепления описывает эвольвенты f₁e₁ и f₂e₂, которые являются искомыми профилями. Для построения эвольвентного профиля зуба первого колеса отрезок AP делим на равные части (в нашем случае на 4). На основной окружности первого колеса вправо и влево от точки A откладываем дуги, длины которых равны этим отрезкам, получаем точки 1', 2', 3', 4', 5', 6' и 7'. Через эти точки проводим касательные к основной окружности радиуса r_b1 (перпендикуляры к соответствующим радиусам). На касательной, проведенной через эту точку 1', отложим 1/4 отрезка AP. На касательной, проведенной через точку 2 отложим 2/4 отрезка AP и т.д. Проведя аналогичные построения на каждой из касательных, получим ряд точек 1'', 2'', 3'',..., 7''.Плавная кривая, проведенная через полученные точки, является эвольвентным профилем правой части зуба первого колеса. Таким же способом строится эвольвентный профиль зуба второго колеса (для этого используется отрезок (BP));

профиль ножки зуба, лежащий внутри основной окружности, очерчивается по радиальной прямой, соединяющей начало эвольвенты с началом колеса, и сопрягается с окружностью впадин закруглением радиуса ρ =0, 4m =0, 4× 9=3, 6 мм

по начальной окружности откладываем половину толщины зуба 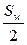, проводим ось симметрии зуба (радиальную прямую) и по законам симметрии строим левый профиль зуба;

- на каждом колесе справа и слева от построенного по точкам зуба строим еще два зуба (с помощью шаблонов или лекал).

При вращении первого колеса (допустим в направлении вращения часовой стрелки) ножка его зуба войдет в зацепление в точке a с головкой зуба второго колеса. В точке b головка зуба первого колеса выйдет из зацепления с ножкой зуба второго колеса. Таким образом, точка зацепления (соприкосновения зубьев) перемещается по профилю зуба первого колеса от его основания к вершине, а по профилю зуба второго - наоборот, от вершины к основанию.

Участки профилей зубьев, которые в процессе передачи вращения входят в соприкосновение друг с другом, называют активными профилями. Определим эти участки. Точку f₁ на профиле зуба первого колеса получим, если из центра O₁ описать дугу O₁a радиусом O₁a. Точно также находим точку f₂, описав дугу O₂b из ценра O₂.

В точке a встретятся точки f₁ и e₂, а в точке b выйдут из зацепления точки e₁ и f₂. Активными профилями являются части эвольвент e₁f₁ и e₂f₂.

Чтобы построить дугу зацепления на первом зубчатом колесе, профиль этого колеса повернем вокруг точки O₁ и совместим последовательно с началом и концом активной линии зацепления, т.е. с точками a и b. На начальной окружности первого колеса получим дугу c'd'. Если повернем профиль зуба второго колеса вокруг точки O₂ и совместим с точками a и b, то на начальной окружности второго колеса получим дугу c''d''. Дуги c'd' и c''d'' являются дугами зацепления по начальным окружностям, дуги ab' и a'b – дугами зацепления по основным окружностям.

Длина дуги зацепления по основной окружности колеса равна длине 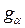активной линии зацепления ab.

Углы j_a1 и j_a2 называются углами перекрытия. Отношение угла перекрытия зубчатого колеса к его угловому шагу t = 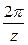называется коэффициентом перекрытия

.

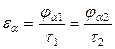Вычислим коэффициент перекрытия проектируемой передачи. Из чертежа длина активной линии зацепления равна 82 мм, что соответствует действительному значению g_a = (ab) = 41 мм. Тогда коэффициент перекрытия

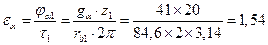
Коэффициент перекрытия можно вычислить также аналитически по формуле

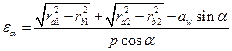
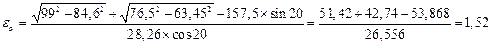
Коэффициент перекрытия показывает среднее число пар зубьев, одновременно находящихся в зацеплении. Если e_a = 1, 52, то 52% времени в зацеплении участвуют две пары зубьев, а 48% времени – одна пара.

Удельное скольжение профилей зубьев (n₁ и n₂) является характеристикой скольжения одного профиля зуба по второму, т.е. характеризует износ профилей, вызванный появлением сил трения.

Удельное скольжение можно определить по формулам

;

;

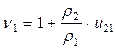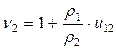где r₁ - радиус кривизны эвольвенты первого колеса в точке зацепления;

r₂ - радиус кривизны эвольвенты второго колеса в точке зацепления;

u₁₂, u₂₁ - передаточное отношение ступени.

Передаточное отношение для внешнего зацепления определяется как

; .

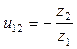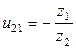Вычислим удельное скольжение в нескольких точках зацепления и построим диаграммы удельного скольжения. Ось абсцисс диаграмм проведем параллельно линии зацепления, а ось ординат перпендикулярно к ней через точку A. Спроектируем на ось абсцисс точки A, a, P, b и B. Тогда r₁ = x, r₂ = g₂-x (g₂ - длина линии зацепления AB).

В нашем случае аb = 82мм в масштабе 2: 1.

;

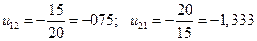Значения текущей координаты X возьмем с интервалом в 15 мм в пределах от X =0 до X =108 мм. Результаты вычислений n₁ и n₂ приведены в таблице

Таблица 5.1- Результаты расчета удельных скольжений профилей зубьев

x=r1
ga-x=r2
n1	-	-7, 26	-2, 47	-0, 87	-0, 07	0, 41	0, 73	0, 96
n2		0, 88	0, 71	0, 46	0, 06	-0, 7	-3, 75	-25, 25	-

Так как зацепление профилей зубьев колес происходит только на активной линии зацепления, то для большей наглядности эти участки заштрихованы.

Толщину зуба первого колеса по окружности вершин определим по формуле 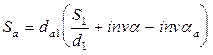, где a_a - угол профиля эвольвенты на окружности вершин зубьев;

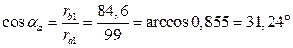
inv 20°=0, 014904; inv 31, 24°=0, 061400

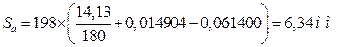
Для нормальной работы зубчатой передачи необходимо, чтобы соблюдались следующие условия:

1) e_a ³ 1, 1;

2) S_a ³ 0, 3 m (отсутствие заострения головки зуба у меньшего колеса).

В нашем случае 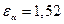и 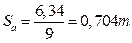, оба условия удовлетворяются.

Таким образом, при решении вопроса относительно выбора и изготовления зубчатой передачи в каждом отдельном случае необходимо исходить из анализа эксплуатационных свойств передачи – продолжительности зацепления и удельного скольжения эвольвентных профилей зубьев.

6. ПРОЕКТИРОВАНИЕ ЗУБЧАТОГО МЕХАНИЗМА