Дифференциальные уравнения первого порядка с разделяющимися переменными.

Уравнение вида f₁(x)j₁(y)dx + f₂(x)j₂(y)dy =0

называется уравнением с разделяющимися переменными. Оно может быть приведено к уравнению с разделенными переменными путем деления обеих его частей на j₁(y) f₂(x):

при условии, что j₁(y) f₂(x) ¹ 0. После сокращения получаем

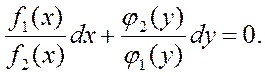(1)

Интегрируя равенство (1), получаем

(2)

где С – произвольная постоянная.

Выражение (2) является общим решением уравнения (1).

Пример. Найти общее и частное решения уравнения dy/dx = - y/x при x = 1, y = 2.

Решение. В уравнении dy/dx = - y/x путем умножения обеих частей на dx разделим (отделим) дифференциалы: dy = -(y/x)dx. Разделив обе части последнего уравнения на у, получим уравнение с разделенными переменными: dy/у = -dx/x. Проинтегрируем его: 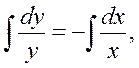откуда

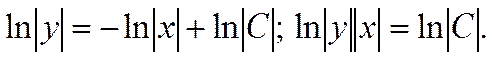
Потенцируя последнее равенство, получаем 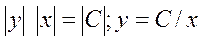- общее решение уравнения.Из условия, что при х = 1 у = 2, найдем значение С: 2 = С/1, откуда С = 2. Частное решение будет иметь вид у = 2/х.

Однородные дифференциальные уравнения первого порядка.

Уравнение dy/dx = f(x, y) называется однородным уравнением первого порядка, если функция f(x, y) может быть представлена как функция отношения своих аргументов: f(x, y)= j(y/x).

Например, уравнение dy/dx = ху/(х² – у²) однородное, так как, разделив числитель и знаменатель правой части на х², получим